Assorted math and logic problems
Questioning is the foundation of all learning.
The first step in rejecting not knowing is to ask, why?
Sweetland
- Logic problems
- Halloween - Which witch?
- Poll problem age of children
- Riddle of the Sphinx
- First number with the letter A
- People names in common
- Geometry & visual spatial relationships -
- Circles
- Angel
- Area Directions
- Drink cups & best deal
- Algebra & patterns
- Pet care
- Infinity
- Functions
- Exponents
- What is your reason
- Number value & operations
- Addition & subtraction
- Division
- Division by zero
- Multiplication 12345678987654321
- Digit
- Card contest
- Data analysis
- Where do we et?
- Comparing additive and multiplicative rates
Logic
Halloween problem
Which witch?
Wilhelmina, Winifred and Wisteria are all witches. Winifred keeps a bat as a pet. Wilhelmina has a broomstick. Wisteria has a black cape and is 300 years old. The witch who can fly is 200 years older that Wisteria. The witch who owns a pet is half as old as is Wilhelmina.
Poll Problem
- A poll taker asked a caregiver the age of the three children under his/her care.
- The person replied that the product of their ages is 36, and the sum of their ages is the same as the next door address.
- The poll taker looked at the address next door and said that she needed more information.
- The caregiver said, "The oldest is upstairs."
- The poll taker said thank you and left.
- What is the age of the three children?
Hint:
- Find all the factors for 36.
- Find eight sets of three with a product of 36.
- Find the sums of the eight sets.
- If the sum is a unique, you will know the answer.
- If it is not, then more information is needed.
- If the older isn't a twin, then you should have it.
Riddle of the Sphinx
What walks on all fours in the morning, on two legs in the afternoon, and on three at night? OH! And if you answer incorrectly the Sphinx will eat you.
What is the first number with the letter A?
If you were to spell out numbers, how far would you have to count until you would find the letter "A"? ......
All the same
What do these people all have in common?
- Alexander the Great
- Attila the Hun
- Smokey the Bear
Geometry and visual spatial reasoning
What's my perimeter?
Seven congruent rectangles make a bigger rectangle.
If the big rectangle has an area of 756 square units, what is its perimeter?
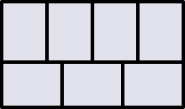
Hint
Think of factors and multiples.
What we know:
- x = width little rectangle
- Y = length of little rectangle
- 4x 8 (x + y) = 756
- 756 / 7 = area of little square
- x * y = area of little square
Circle Problems
If you hold a quarter stationary and roll a dime around the perimeter of the quarter, how many revolutions will the dime make?
If a circle has a circumference of three and a smaller circle of circumference one roles around the larger one how many revolutions will it make?
Angles
What is the sum of all the vertex angles in a triangle?
What is the sum of all the vertex angles in a square?
What is the sum of all the vertex angles in a pentagon?
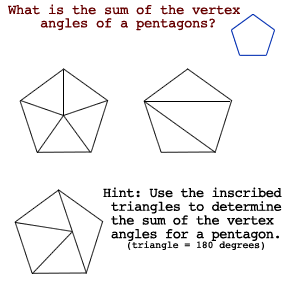
Medial triangles
What are medial triangles?
Focus questions
- Is a mdeial triangle similar to the original triangle?
- What is the relationship of the original side to its corresponding side?
- How does the consruction relate to the triangles it creates?
- Explore filling a triangle with medial triangles. What relationsips can you determine?
Image sources and challenge sheet
Hint:
A medial triangle is the triangle formed by connecting the three midpoints of larger triangle.
Checks
- Is a mdeial triangle similar to the original triangle? They are similar to the original triangle, with a side length ratio of 1:2.
- What is the relationship of the original side to its corresponding side? The sides are parallel to the original triangle's corresponding sides.
- How does the consruction relate to the triangles it creates? It creates four smaller triangles that are all congruent.
Find the area of floor plan

Directions home?

A person leaves home and walks sraight for a mile or so, turns left, walks another mile or so, turns left, and walks for another mile or so and arrives back home, sees two masked people, and knows they are safe and feels great!
Who are the masked people?
Bonus: Explain what is wrong or unusual about the illustraion.
Drink cups
Hot drink cups at one store come in four sizes:
- Short 8 fl. oz.; or 240 ml
- Tall 12 fl. oz.; or 350 ml
- Grande 16 fl. oz.; or 470 ml
- Venti 20 fl. oz.; or 590 ml
Approximately what are the dimensions for each cup size?
- .577 fluid ounces are in one cubic inch
- 1 ml = to 1 cubic centimeter of water
Select inches or centimeters and design some cups. Describe how your design will almost be filled with the appropriate amount.
Algebra
Patterns
Pet care and sequences
Your neighbor family is going on a vacation for thirty days and ask you take care of their family pet. Since the family pet is very valuable they are concerned it gets very good care. They explain this to you and ask which method of payment you would prefer.
- $10, 000 a day for each day they are gone and the pet lives.
- $.01 the first day, $.02 the second day, $.04 the third day, $.08 the fourth day and so on for each day the pet lives.
You are not concerned about the pet dying, since you will take very good care of it. Assuming the pet lives all thirty days which plan will you take to make the most money?
Infinity
Why is .999999... equal to 1?
Explain to the student who says.
"Shouldn't it be equal to .0000000000 ... 1? I mean if you compare the two there should be a difference of one somethingth. Shouldn't there be?"
Functions
If you have the function 2n + 1
What is n?
What do you want it to be?
It is a function, it can be whatever you want it to be.
Try some numbers ...
Like, 0, 1, 2, 3, 4,
If you do you get the set ...
1, 3, 5, 7, 9...
Are they infinite?
How can the set of whole numbers and the function 2n + 1, set both be infinite? It woul seem that one-half the other ...
Consider the function, 2x + 1. (Note: other letters could be used instead of x, like n ...)
When this function turns up in the world it usually represents odd numbers.
What about a function for x squared?
What about a function for x squared and z squared?
Are they always squares?
Exponents
If 32 is 3*3 = 9 or the product of two threes as factors, then shouldn't 30 be the product of one three zero times or zero?
What's your reason?
There are 100 centimeters in a meter.
So support or reject 100 cm = 1 m as a valid or invalid statement?
Rate
Consider how fast different animals are and calculate how long it would take the to travel a certain distance. What would a graph look like?
Example
If a cat can run 44 feet per second, how far would it run in 12 seconds?
Number value and basic operations
Addition & subtraction
Three and Five bucket problem
A person has a three and five liters bucket and needs to measure four liters. How can it be done?
Hint: Look here for hints, more bucket problems, and proof ...
Digit
Subtract nine digits which total 45 from nine digits that also total 45 and have a difference of nine digits which also has a total of 45.
Multiplication and division
Division
A person wants to put 14 cookies on a plate and has 169 cookies. How many plates can be filled? or How many 14's are in 169? Represent the problem with diagrams. One with plates and another with one hundred square, ten rods, and one cubes.
Division by zero
If 6 / 2 = 3 because six cookies divided onto two plates means there is three cookies on each plate.
Therefore 3 / 0 would be three divided onto zero plates would be ...?
What two numbers can be multiplied to get 12,345,678,987,654,321?
Answer: 111,111,111 x 111,111,111
Card Contest
A collector can win a contest for 100 baseball cards if they can solve this problem. They will be given $100.00 to purchase 100 cards if they can figure how to select cards from three groups so that the total for 100 cards will be exactly $100.00.
The cards must be selected from only three groups which costs are:
- Group one, $.50
- Group two, $3.00
- Group three, $10.00
How many from each group can be bought and what is each group's total cost for 100 cards at $100.00?
Combined operations
Plan a river trip

Fee/Person (includes PFD, paddles, transportation to launch site. All trips end at Sunny Brook Camp landing)
All children taking their own solo kayak or tube pay full per person rate.
Following times are for canoe & kayak trips.
Double the time for tube trips.
- $50 - 6 hours - Cornell Bridge / Ft. Niobrara NWR Canoe Lunch Site
- *$2.00 USFWS USER FEE PER PERSON, ADDITIONAL
- $50 - 3 hours - Smith Falls State Park / Nichols Landing
- $40 - 2 hours - Brewer Bridge / NRD Public Use Area
- $30 - 1 hour or less (various trips offered)
- $55 - 4 hours - Berry to Sunny Brook, $10 LAUNCH FEE PER VESSEL ADDITIONAL
- $15 per cooler tube
Challenge:
Plan a family or class trip.
Bonus:
Use a map and find how long each trip is. What is the rate per mile for the different trips?
Let's raise some money
![]()
You have two weeks to raise money for ____________.
If you bake a batch of 64 cookies each day and put four per bag, how many cookies can you sell?
Challenge:
You got the ingredients donated so whatever you see the cookies for can be used to donate to your cause.
How much would it be if you charged $.50 a cookie, $.75 a cookie, and $1.00 a cookie?
Let's eat
Use the question, "What is your favorate place to go and eat?"
Poll the class. Could use the poll and the information for a data analysis activity.
For this activity get or find online menus for the selections.
Ask. What kinds of problems can we solve with these menus?
What is the least expensive item?
What is the most expensive item?
What would it cost if we ordered one entre´e, one side _________, and a drink for everyone in your group/class?
If we had a ________________ party where would you recommend we order from and why?
What does times the price mean?
What does BOGO mean?
Fractional numbers
Marshmellow treats for everyone
Recipe
3 1/8 cups mrshmellows
4 3/4 cup rice cereal
1/8 cup butter
The recipe serves eight.
Challenge:
What would be the recipe for a class of 24?
Which is greater?
A clasmate thinks 1/5 is larger than 1/4 because five is greater than four. Are they correct? How can you demonstrate the value of each and explain if you agree or disagree?
Data analysis
Let's eat
Use the question,
How can we find out what are the most favorate places for us to go and eat?
Decide what questions to use to poll the class.
Select three or so to poll the class.
Ask. How will we process the data?
Decide to chart the data, find the mean, median, mode, graph ...
Collect the data.
Process the results.
Comparing additive and multiplicative rates
Need to make a problem for the following:
Using the data below. Determine how many more times a person was likely to die from COVID-19 than from influenza in 2020.
April 2020 the estimated death rate for influenze was 0.1% and for COVID-19 it was 2.1%.
A person who interprets these as additive as a 2.0% differance may not see it as that much more deadly. However, if a person compares it as multiplicative they will conclude that COVID-19 is 21 more times as deadly as influenza. Thus reaching a more meaningful comparison.