Carnival gaming
Carnival fun!
Questioning is the beginning of understanding!
Franklin
Overview
- Introduction
- Agenda
- Situation 1 - Three coin toss resources
- Situation 2 - Decide Which rides
- Situation 3 - Over, Under, & 7
- Situation 4 - Ball Roll Game
- Situation 5 - Spinner Game
- Situation 6 - Plink o ham game
- Situation 7 -
Introduction
This page includes a carnival math adventure where you can follow the agenda and experience different carnival situations to wonder and explain. If you have no background with probability you might want a review these six probability activities first.
Agenda
- You arrive at the ticket office and buy a book of 2o tickets for the carnival rides.
- As you walk toward the midway you approach the Police Chief, Arthur Smart and his partner Cal Q Letter. They are talking to Norman who is irate with the three coin toss vendor. You are intrigued, slow down, and eaves drop on what is going on.
- They are pointing to the sign for the game.
- You listen in ...
Situation 1
Catch-up on the conversation by reading the Reader's Theatre - Case of the Carnival Probability game.
Resources to figure out what Cal did.
- Example of a three coin toss - video.
- Game sign with rules of play
- Hints - probability, theoretical, experimental and how to use them
- Summary example of 48 games played
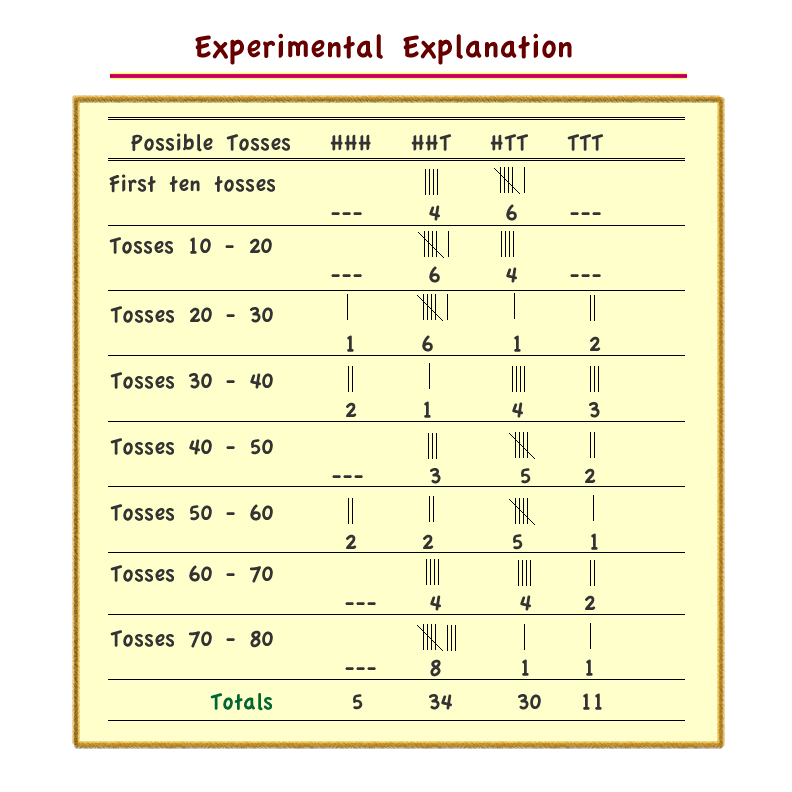
- Experimental representation of 48 games played.
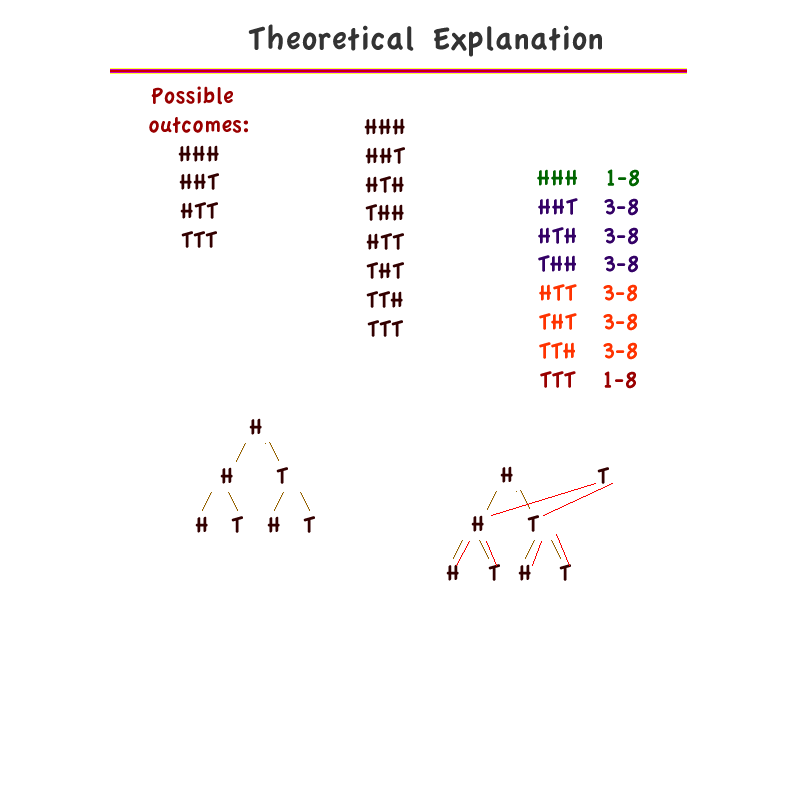
- Theoretical representation of 48 games played.
- Explain why Cal represented the problem theoretical.
- Explain why Norm represented the problem experimentally.
- Explain why the game was not fair.
- After listening and seeing the Police in action, you are glad they are on the job and head to the midway.
- When you get there, you remember the different rides take different numbers of tickets, that you bought earlier. You wanted to ride each ride at least once and you knew twenty tickets would be enough with some left over. So now you think about how you might decide which ones you want to ride with the twenty tickets.
Situation 2
- Decide Which rides you could ride?
- Hints with workspace
- What combinations are possible?
- Identify three combinations that are not possible.
- As you pass the Luck 7 - over & under booth, you slow down and check out the action.
Situation 3
- Check out the Over, Under, & 7 Booth
- Make observations of the game rules and watch a few games being played.
- Decide if the payout of $2.00 and $5.00 makes it a fair game.
- If it isn't, what payout should be offered?
- Hints and worksheet to explore combinations for the sum of two dice.
Hints:
- The sums of the die are: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
- Possible sums.
- 2 = 1+1,
- 3 = 1+2; 2+1;
- 4 = 1+3; 2+2, 3+1,
- 5 = 1 + 4; 2 + 3; 3 + 2; 4 + 1
- 6 = 1 + 5; 2 + 4; 3 + 3; 4 + 2; 5 + 1
- 7 = 1 + 6; 2 + 5; 3 + 4; 4 + 3; 5 + 2; 6 + 1
- 8 = 2 + 6; 3 + 5; 4 + 4; 4 + 4; 5 + 3; 6 + 2
- 9 = 3 + 6; 4 + 5; 5 + 4; 6 + 3
- 10 = 4 + 6; 5 + 5; 6 + 4
- 11 = 5 + 6; 6 + 5
- 12 = 6 + 6
There is
- One way for the dice to have a sum of 2,
- Two for 3
- Three for 4
- Four for 5
- Five for 6
- Six for 7
- Five for 8
- Four for 9
- Three for 10
- Two for 11
- One for 12
For a total of 36.
Under 7 = 15; Over 7 = 15; & 7 = 6
- As you pass the Ball roll and stop on what color booth, you slow down and check out the action. Dot grid
Situation 4
- Check out the Ball Roll Game booth
- You wonder what the pay out should be.
- If there are seven colors placed randomly throughout the game board that has seven by seven colored holes for the ball to rest in.
- Dot worksheet.
- You think to be fair, theoretically, it should pay out $7.00 for each dollar bet on any color that the ball lands on.
- You wonder if it actually works out that way ... experimentally.
- Then you wonder what kind of kind of game you could make if the colors weren't evenly divided. Like if there were one color out of 49 and it would pay out 49:1. Wow!
- You wish the square had fifty holes so it wold make the math nicer. What about a 10 X 5 playing board?
- Design your own game and identify the theoretical probability for each color you use on your playing board.
Situation 5
- Check out the Spinner Game booth
- This spinner has nine equal sections with different colors. Two with duplicate sections.
- You can use this spinner set up or design your own for your game.
- Be ready to explain the theoretical outcomes and probabilities.
- You could make your own spinner and experiment to find an experimental probability for it. See more information about spinner patterns & spinner patterns.
Situation 6
- Check out the Plink o ham game.
- The ham plink o game is a game with a history. It has been part of the carnival since the carnival started. A local food market wanted everyone, who might be short of money, to leave the carnival with a ham for their family. So they got a local supplier to provide them with hams at cost. So they figured they could afford to pay out one ham for every two times someone played. However, they weren't sure how much to charge to play or what exactly the payout outcome would be. SO this year they started with $3.00 to play and found it was a bit over priced, if the outcome was 50:50, so they lowered it to $2.00. Hoping the average ham could be won for $4.00. Which would be slightly below cost.
- Decide if the set up of the Plink o game board will achieve their goal. Or another ham should be added.
Situation 7
- Make your own situation as a culmination for your adventure.
When you go to a carnival or a similar venue, What do you enjoy more, the rides or the games!
Three coin toss game
Three coins toss example
Example 3 coin toss game
Hints
Probability can be guessed perceptually or determined theoretically or experimentally.
Either way, you need to determine all the possible outcomes for the particular event. This means systematically figuring out all possible combinations (combinatorial representation), and comparing each outcome or group of outcomes as proportions of all possible outcomes.
Perceptually young children describe probability comparing visual representations, which may be done accurately or not, depending on their development. They may be fooled by thinking a certain amount is more or less if they are not able to conserve. It looks like there are more red so I will guess red. So young children begin to determine probability by visual comparison and using more, less, or none to equate to probabilistic terms of likely or probable, not likely, as certain, possible, impossible. Perceptually is thinking that two heads is twice as hard to toss because it takes two to win.
However, being able to conserve and accurately determining cardinality isn't sufficient to determine probability as mentioned above.
Experimental is what Norman used and theoretical is probably what Cal used by making a combinatorial representation in his notebook.
The Case of the Carnival Probability Game
The Cast:
- Police Chief
- Vendor
- Cousin Norman
- Cal Q. Letter
- Narrator
- Three coin toss
- Three coin toss sign
The Story
Narrator: The smells of buttered popcorn, cotton candy, and fried dough filled the air as Midville Police Chief Arthur Smart and his partner, 12-year old detective Cal Q. Letter, passed through the gates of the 85th annual Midville Fair. The Chief had been asked to participate in the pie-eating contest, and Cal had tagged along to support him.
Chief: "You know, it's gonna be difficult to stick to my diet today". He stopped in front of Perry's Pizza booth. "Maybe I'll have just a tiny slice of pizza before the contest".
Cal: "Do you really think that's a good idea, Chief?"
Narrator: Chief blurts out.
Chief: "Hey, look. That's my cousin Norman arguing with that vendor over there."
Narrator: Cal looked across the way and spotted a short, pudgy man who could pass for the Chief's twin gesturing wildly and stomping up and down. The Chief and Cal rushed over to see what the commotion was all about. The vendor, a lanky man with long sideburns, stood behind his counter, shaking his head smugly.
Vendor: (Points to Cousin Norman) "You lost, fair and square."
Chief: (Placing a hand on Norman's shoulder) "Norman, what's going on here? I've never seen you this angry."
Norman: "I'll tell you what's going on here" (Grits his teeth) "A big time ripoff! This guy here is running some sort of crooked scam. I just can't figure out how he's doing it."
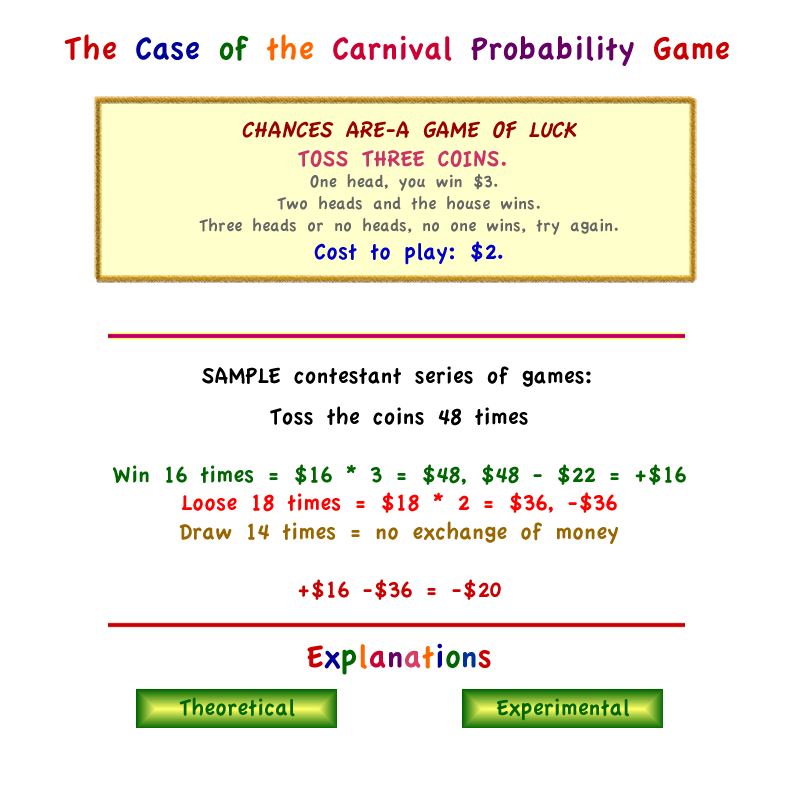
Narrator: Cal looked up at the sign over the booth. It read: "CHANCES ARE - A GAME OF LUCK. Toss three coins. One head, you win $3. Two heads and the vendor wins Three heads or no heads, no one wins, and we roll again. Cost to play: $2."
Chief: "Let me get this straight; let's say you play once and win. It cost you $2 to play, and you won $3, so you really made $1. Isn't that right, Cal?"
Narrator: Cal nodded and began drawing a diagram in his math notebook.
Chief: "And if you lose, you lose the $2 you paid to play, right?"
Narrator: Again Cal nodded.
Vendor: "Look, it's twice as hard to get two heads as it is to get one head. That's why it's a fair deal that if I win, I get twice as much as when I lose."
Chief: "Makes sense to me."
Norman: "Wait, I've played this game 48 times. I've won 16 times, he's won 18 times; neither of us won 14 times. I've lost $20 to this schemer. That shouldn't happen, should it?"
Vendor: (With a smirk) "Hey haven't you heard of a lucky streak?"
Narrator: The Chief picked up the three coins from the counter and carefully examined each of them.
Chief: "Nothing's wrong with the coins, Norman. Look, I'm sorry you lost, but it appears that this just wasn't your day. That's all."
Norman: "It doesn't make sense. Probability says I should have won twice as often as he did and that we should have broken even money-wise, doesn't it?"
Cal: "No, it doesn't. In fact, things pretty much went according to probability. Your cousin is not correct about probability, but he is correct about one thing: This game is a ripoff. Big time. This vendor has a guaranteed winner with his game."
Chief: "Well, that's enough for me." Turning to the vendor: "You, sir are shutting down and coming downtown with us."
How is this game unfair? What did Cal figure out?
Ticket office
Midway
Which rides?
What rides do you want to ride with your twenty tickets?
| Tickets per ride | P use 1 | P use 2 | P use 3 | P use 4 | P use 5 | P use 6 | P use 7 | P use 7 | P use 8 |
|---|---|---|---|---|---|---|---|---|---|
| Ferris wheel - one ticket | |||||||||
| Carousel - two tickets | |||||||||
| Bumper cars - three tickets | |||||||||
| Roller coaster - five tickets | |||||||||
| Total number of tickets used |
Work space for ride choices
Hints:
Think - theoretical solution.
If you use one ticket for each ride that will take 11 tickets.
Leaving 9 left for additional rides.
| Tickets per ride | P use 1 |
|---|---|
| Ferris wheel - one ticket | 1 - 1 |
| Carousel - two tickets | 1 - 2 |
| Bumper cars - three tickets | 1 - 3 |
| Roller coaster - five tickets | 1 - 5 |
| Total number of tickets used | 11 |
Which means you don't have enough to ride each ride a second time.
You could ride the bumper cars three more times - P use 1.
You like the bumper cars but your not sure you want to ride them three times. So figure what else you might ride with two or one.
Table with focus on bumper cars
| Tickets per ride | P use 1 | P use 2 | P use 3 | P use 4 | P use 5 | P use 6 | P use 7 | P use 7 | P use 8 |
|---|---|---|---|---|---|---|---|---|---|
| Ferris wheel - one ticket | 0 | 1 - 1 | 1 - 1 | ||||||
| Carousel - two tickets | 0 | 1 - 2 | |||||||
| Bumper cars - three tickets | 3 - 9 | 2 - 6 | 1 - 3 | ||||||
| Roller coaster - five tickets | 0 | 0 | 1 - 5 | ||||||
| Total number of tickets used | 9 | 9 | 9 |
Table with focus on Carousel
| Tickets per ride | P use 1 | P use 2 | P use 3 | P use 4 | P use 5 | P use 6 | P use 7 | P use 7 | P use 8 |
|---|---|---|---|---|---|---|---|---|---|
| Ferris wheel - one ticket | |||||||||
| Carousel - two tickets | |||||||||
| Bumper cars - three tickets | |||||||||
| Roller coaster - five tickets | |||||||||
| Total number of tickets used |
Table with focus on Ferris Wheel
| Tickets per ride | P use 1 | P use 2 | P use 3 | P use 4 | P use 5 | P use 6 | P use 7 | P use 7 | P use 8 |
|---|---|---|---|---|---|---|---|---|---|
| Ferris wheel - one ticket | |||||||||
| Carousel - two tickets | |||||||||
| Bumper cars - three tickets | |||||||||
| Roller coaster - five tickets | |||||||||
| Total number of tickets used |
Table with focus on Roller Coaster
| Tickets per ride | P use 1 | P use 2 | P use 3 | P use 4 | P use 5 | P use 6 | P use 7 | P use 7 | P use 8 |
|---|---|---|---|---|---|---|---|---|---|
| Ferris wheel - one ticket | |||||||||
| Carousel - two tickets | |||||||||
| Bumper cars - three tickets | |||||||||
| Roller coaster - five tickets | |||||||||
| Total number of tickets used |
What are all possible combinations?
Lucky 7 - Over & Under booth ...
Game observation
You see and hear.
The barker call out to people to play lucky seven. And place a $1.00 bill on a Lucky seven square.
Watching, you see players place $1.00 on their chosen square of the board.
And notice the sign and conclude how the game is played.
They are betting $1.00 by placing it on one of three squares.
WINNERS will win
- $2.00 if they bet on under and it comes up 2, 3, 4, 5, or 6
- $5.00 if they bet on 7 and it comes 7
- $2.00 if they bet on over and it comes up 8, 9, 10, 11, or 12
or as the sign says.
- Under 7: - Betting the dice total will be less than 7
- Lucky 7: - Betting the dice total will be 7
- Over 7: - Betting the dice total will be more than 7
Once all bets are placed, the barker rolls the dice.
Announces the sum of both die as the result and announces the winner as OVER.
Removes all the $1.00 bills off the UNDER and 7 squares, as they didn't win.
Pays the players by placing a $1.00 bill on top of the $1.00 bet on the OVER square.
The game ends and the barker calls for players to place a $1.00 on a square.
You summarize what you saw and didn't see as.
- Under 7, Must mean that if the total is less than 7, the house pays $2.00 to all players on Under 7. All other players lost $1.00.
- 7, Must mean that if the total is exactly 7, the house pays $5.00 to all players on Under 7. All other players lost $1.00.
- Over, Must mean that if the total is more than 7, the house pays $2.00 to all players on Over 7. All other players lost $1.00.
As you leave you wonder, Is 7 the Lucky number or not?
How can you explore if there are odds that are favorable for a player.
Worksheet for over and under 7
| Roll | Ways to get the rolled number |
|---|---|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
Ball roll game
Dot grid 7 x 7
Dot grid 10 X 5
Carnival spinner booth
Activities to explore spinners
Ham Plink o Board
