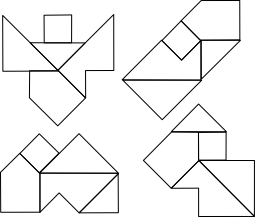
Five - Five Piece Puzzles
Directions: The five pieces can be used for five puzzles. The first puzzle uses all five pieces to make a square.
Hint 1: Different sizes of squares can be made with some or all of the pieces. However, a square can be made that uses all five pieces, side by side, with none of the pieces on top or over lapping another piece.
Five square puzzle pieces
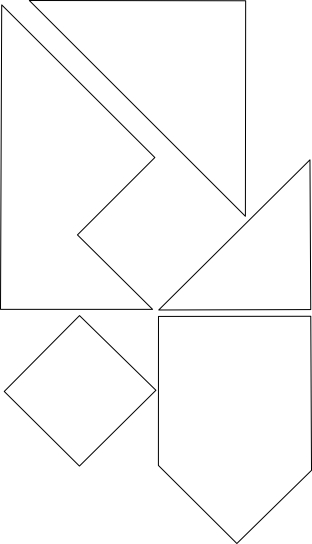
Hints and more
Most people, on their first attempt, make a square with four pieces and have one piece left over. Think about what that means. For one thing it means the size of the square made with four pieces, has a smaller area than one that can be made with five pieces.
Okay, that is obvious when you think about it. However, look at the pieces used to make the square. I bet, without me looking at it, that the longest side of any piece in your four piece square is positioned with that longest side as an edge of the square.
Flash of enlightenment!?
If the longest side of any piece can't make a square big enough (in area) to fit all five pieces, then to fit all five pieces into the square, every side must have more than one side of each piece that makes up every side of the square.
In other words: two sides of every shape must be used to make each side.
Wow!
Is that counter intuitive or what?
I struggled with that.
So think about how the pieces could be positioned with the longer sides not as an edge.
Math stars
If you label one side of the pieces X , then what would all the other sides of all the figures be relative to that side (x)? If you do, then you'll have a new respect for squares, square roots, and Pythagoras.
Wow!
Last hint: Square puzzle solution
Four more five piece puzzles.
Use the five pieces to make the following shapes:
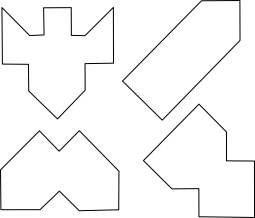
Two Puzzles
Solutions
Square puzzle solution

Four puzzle solutions