Triangle exploration and investigation activities
Introduction:
Activities include ideas related to geometry, patterns, problem solving, reasoning, visual representation, trigonometry, and other mathematical ideas
Trigonometry is the study of triangles and the relations of their sides and angles.
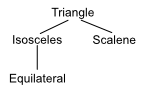
A triangle is a plane closed figure with three straight sides and three angles. There are three kinds based on the length of their sides.
- Equilateral - three equal length sides.
- Isosceles - two equal length sides.
- Scalene - all sides are different lengths.
Activity ideas
Kinds of triangles
- Ask. What is a triangle?
- List properties of a triangle.
- Sort shapes into triangle and not triangle.
- Identify triangle shapes in images of objects in media and trace their perimeters.
- Identify different types of triangles.
- Define triangles as equilateral, isosceles, and scalene.
- Explain the triangle tree and make an equivalent Venn diagram.
- Make artistic designs with triangles.
Triangle forensics
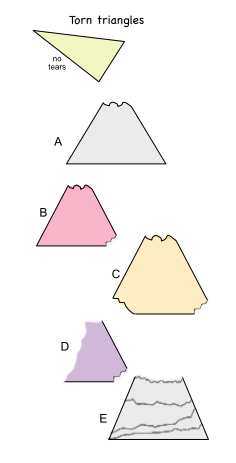
Can a triangle be recovered from it's parts?
- Draw a triangle on a sheet of paper and cut it out.
- Cut a corner (vertex) off of it.
- Using what is left of the triangle, could another person use it to draw a congruent representation of the original triangle?
- How much of an original triangle can be removed (torn off) and a person could know what the original triangle was? one corner, two corners, three corners
- What if a corner and a whole side were removed?
- Make a rule that describes what the least amount of information needs to be known to make a known triangle. (A know angle, side, angle to find 2 sides and angle; B know angle, don't know any sides or other 2 angles, but can extend the side opposite the known angle to determine them; C don't know any side or angle, but can determine them by extending all the sides; D don't know any side or angle, but can extend two sides and determine one angle, but need more information to know how long the two side pieces should be extender; E know two angles and one side, can use them to determine the rest.)
- How does this information relate to the congruency tests of triangles? (side, side, side; side, angle, side; angle, side, angle; angle, angle, side)
Can triangles be made with any length sides?
What lengths of sides will make triangles? Use straws, toothpicks, strips of paper, Cuisenaire rods, or other appropriate objects and make a list of combination of lengths that will make triangles and those which will not.
To start focus your investigation by limiting the length of the sides by focusing on 3 cm lengths and see what whole number lengths can be used with it to make triangles.
Let's start with all the sides 3 cm. Will that make a triangle?
Attempt |
Side 1 | Side 2 | Side 3 | Triangle |
|---|---|---|---|---|
| A | 3 cm | 3 cm | 3 cm | Yes - No |
Next. Let's try 3 cm on two sides. What whole number combinations will make a triangle?
Attempt |
Side 1 | Side 2 | Side 3 | Triangle |
|---|---|---|---|---|
| B | 3 cm | 3 cm | 1 cm | Yes - No |
| C | 3 cm | 3 cm | 2 cm | Yes - No |
| D | 3 cm | 3 cm | 4 cm | Yes - No |
| E | 3 cm | 3 cm | 5 cm | Yes - No |
| F | 3 cm | 3 cm | 6 cm | Yes - No |
| G | 3 cm | 3 cm | 7 cm | Yes - No |
Summary
What did you discover?
If some combinations don't work, why didn't they?
Now let's try 3 cm on one side. What whole number combinations will make a triangle?
Attempt |
Side 1 | Side 2 | Side 3 | Triangle |
|---|---|---|---|---|
| H | 3 cm | Yes - No | ||
| I | 3 cm | Yes - No | ||
| J | 3 cm | Yes - No | ||
| K | 3 cm | Yes - No | ||
| L | 3 cm | Yes - No | ||
| M | 3 cm | Yes - No | ||
| N | 3 cm | Yes - No | ||
| O | 3 cm | Yes - No |
Summary:
What did you discover?
If some combinations don't work, why didn't they?
What conjecture can be made about sides of equal lengths (equilateral) and triangles? Any length of a side can be used to make equilateral triangles.
What conjecture can be made about sides of triangles with two sides equal (isosceles)? The third side of an isosceles triangle is less than the sum of the two sides.
What conjecture can be made about the relationship of one side of a triangle to the other two sides?
Triangle angles
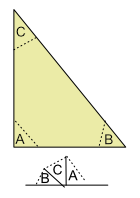 Questions:
Questions:
- What is the sum of the three angles of a triangle?
- Do all triangles have the same angles?
- Is the sum of the angles the same for all triangles?
- How can I have confidence in my answers?
Use a ruler and draw a fairly large triangle on a sheet of paper. Tear off the corners (angles, vertices) and place them together along a line. Does the sum of the angles match the line.
- How many degrees is the line?
- How many degrees is the sum of the triangles angles?
- What is a three sixty dunk?
- How does the degree of a line relate to a 360 dunk?
Use a protractor to measure the angles, add them and see how close it is to 180°.
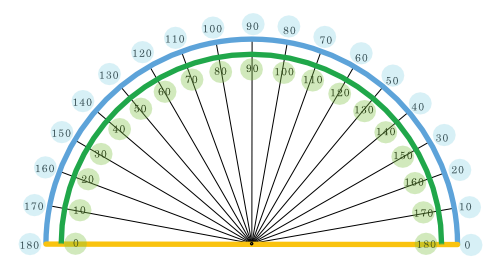

Making a triangle from three angles
The set up
- Get a sheet of paper.
- Put a dot at about the center of one edge.
- Don't need to be accurate. Cut out a semicircle with the dot toward the center of the diameter edge of the semicircle.
- Use the dot as a vertex to cut the semicircle into three pieces or three angles.
- Use the three pieces and make a triangle with each angle as a vertex of the triangle.
- What can be concluded about knowing three angles to make a triangle?
Summary
Changing sides & angles proportionally
What happens to the shape of triangles when their angles and sides are changed?
It seems obvious when an angle or side is changed, the other two sides or angles have to change for the shape to be a triangle. Here are some changes to explore:
- Keep one angle and one side constant. Change a second angle and record how the other two sides and angle change.
Triangle |
Angle manipulated | Angle not changed | Angle responding | Side not changed | Side responding | Side responding |
|---|---|---|---|---|---|---|
| Start | 15° | 90° | 3 cm | |||
| Double once | 30° | 90° | 3 cm | |||
| Double twice | 60° | 90° | 3 cm |
Summary
Write conjectures as if, then statements.
If angle A increases, then ...
If angle A is the largest angle, then side a is ...
If angle A is the smallest angle, the side a is ...
What's my angle
What is the relationship of angles in triangles?
Find the angles for the triangle information in the table.
Side a is opposite angle A, b opposite B, and c opposite C. hint: make a drawing.
Triangle |
Angle A | Angle B | Angle C | Side a | Side b | Side c |
|---|---|---|---|---|---|---|
| A | 50° | 60° | ° | |||
| B | 32° | 108° | ° | |||
| C | ° | ° | ° | a = b= c | b = a= c | c = a= b |
| D | 66° | ° | ° | a = b | b = a | |
| E | 90° | 30° | ° | |||
| F | ° | 45° | ° | b = c | c = b |
What triangle angles will tessellate in a circle fully?
Select a triangle and one of its angles. Place it in the middle of a piece of paper with the selected angle at the center of the circle. Trace it. Rotate it right or left the number of degrees of the angle, then trace it again. Continue until you get to the beginning. Did it rotate a perfect 360?
Try other triangles and find what kinds of shapes the different triangles make.
Which shapes are used in designs?
What would happen if you switched different triangles?
Try it and find shapes and patterns you like.
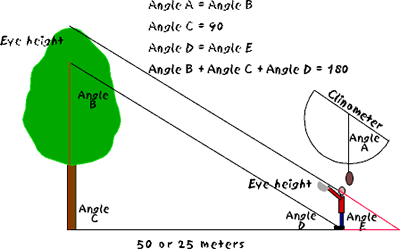
Using two angles and a side to find another side
Problem types: measuring the height of building, towers, trees, ...
Information: we know the tree, building or tower should be perpendicular to the Earth (90). We can pace or measure a certain distance from the base of the tree or other object to determine a side. Then use a clinometer to find the angle at that point a line would make drawn from that point to the top of the tree or building. How to make and use a clinometer to measure height.
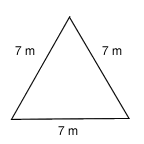
Triangle perimeter
What is the perimeter of the triangle?
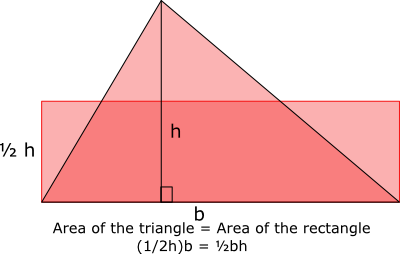
Triangle area
Use the diagram to find a formula for the area of a triangle.
b = 46; h = 26; 1/2 h = 13