Fractions: Counting by three-fifths
We don’t need no more rappers don’t need no more basketball players, no more football players. We need more thinkers. We need more scientists. We need more managers. We need more mathematicians. We need more teachers.
WE NEED MORE PEOPLE WHO CARE.
Tupac Shakur
Challenge:
Count by 3/5's and explore patterns in the sequence of groups of three-fifths. ![]()
Hint:
- Count by 3/5s.
- Make a list of groups of three-fifths.
- What do you notice about the numbers?
- Organize them into rows with each row starting with a whole number equivalent.
- What patterns do you notice?
Discussion:
Count orally: three-fifths, six-fifths, nine-fifths, twelve-fifths, fifteen-fifths, eighteen-fifths, ...
Record the group and number of fifths in each group ...
| Number of groups | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total |
| Number of groups | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total |
Patterns for the denominator ...
Patterns for the numerator ...
What about group 100?
Group ...
What patterns can you find when you arrange them in a grid starting a new row for each whole number equivalent. Like below.

Sample with some notes
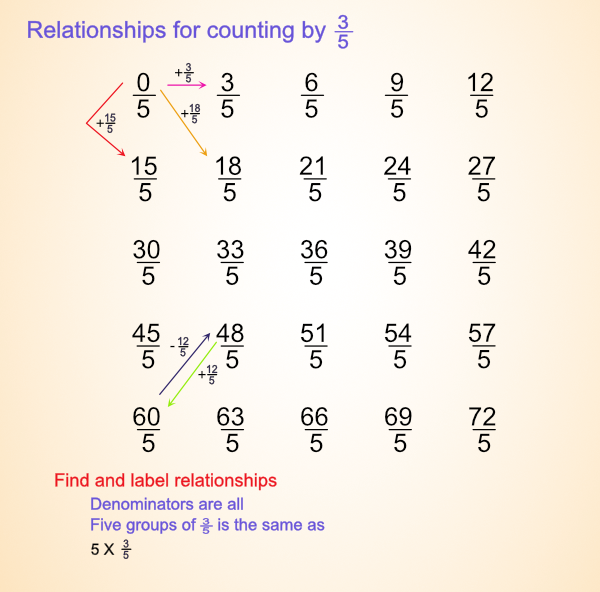
Some patterns:
- Denominators are all fifths.
- Numerators ar 0, 3, 6, 9, 12, ...
- Numerators add three each tme.
- Numerators are multiple of three.
- Numerators are odd, even, odd, even, ...
- You add 15 going down each column.
- You add 18/5 diagonally.
- Five groups of three (15/5) are the same as three.
- Ten groups of 3/5 are the same as six.
- Number in ones place in each column alternate. (0,5; 3,8; 6,1; 9,4; 2,7).
What will a graph look like for the relationship for groups and number of fifths?
What will be the difference if the number of groups are graphed as x-values and totals as y-values vs. the number of groups as y-values and totals as x-values.
Graph
