
Mathematical Knowledge base:
Concepts, misconceptions, outcomes, & standards to plan and facilitate mathematical literacy & critical thinking
Concepts must be caught not taught!!!
- Introduction
- Algebra & patterns
- Attitudinal (disposition & value statements)
- Classification
- Communication
- Connections & perspective
- Data Analysis & probability
- amp
- Measurement
- Number value
- Operations
- Problem solving
- Reasoning & proof
- Relative Position and Motion
- Variable
Introduction
A mathematical knowledge base provides information to develop math literacy. Information, a person knows and uses to be science literate, which can be organized into the dimensions of science and communicated as concepts and organized into five dimensions:
- Dispositions, attitudes, habits of mind, & values to attain positive mathematical practices
- Practice of mathematizing
- Processes & process skills
- Content areas: Number value, algebra & patterns, measurement, geometry, & data analysis
- Perspectives: Engineering & technology, personal & social, history of math, nature of math.
These dimension and some subdimensions are illustrated in the following model or diagram:
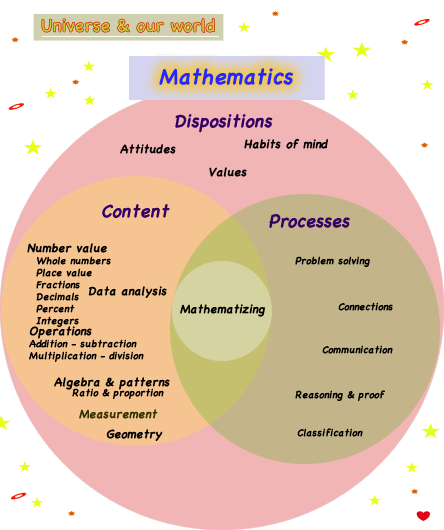
These dimension and subdimensions are used to organize information as misconceptions and three levels of concepts: beginning, literate, and advanced. The table below outlines this organization:
Misconceptions and concepts
Initial perceptual naive misconceptions (all ages)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Misconception list
Beginning concepts (preschool - 7 years) ... list
Literate concepts (middle level to adult) ... list
Advanced concepts ... list
Educator notes

Algebra and patterns
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
Explanations for people's misconceptions: naive understandings & perceptual responses)
- School math is different than math used outside of school.
- Patterns with numbers are different than patterns with physical objects.
- Equals symbol means solve.
- Two negatives make a positive.
- Multiply everything inside the parentheses by the number outside the parentheses.
- Always use PEMDAS (Please Excuse My Dear Aunt Sally).
Beginning concepts (preschool - 7 years)
- Number values can represent objects (first, one,) and properties of those objects.
- Number values can represent ideas and properties of those objects.
- Sets can be equal or not equal.
- Sets can be copied.
- Logical patterns exist and occur regularly in mathematics.
- Patterns can be copied ( ordered sets, objects..).
- Patterns can be recognized, extended, or generalized.
- The same pattern can be found in many forms.
- Patterns are found in nature and physical objects as well as numbers.
- Patterns can be described, represented, and communicated in a mathematical way.
- Simple patterns can be recognized in more complicated patterns
- Classification is helpful when searching for patterns
Literate concepts (middle level to adult)
Algebra: patterns, equations, and functions
- A system can have any number of equations and any number of variables.
- When there are only two variables it is possible to visualize the relationship with a graph on a coordinate plane.
- Graphs are pictorial representations of information
- Each person in the world could pick a different three points on a line, because there are infinite ordered pairs as solutions for any line. All of which will graphed the same line.
- Simultaneous equations can be represented with graphs.
- Systems of equations are dependent, consistent and independent.
- Substitution and elimination methods can be used to solve simultaneous equations.
- A system of equations is two equations that share variables.
x + y =10; -3x + y = 2 - A system of equations can be represented graphically in different ways:
- Solution set/feasible region.
- Applying Systems of Equations to application problems.
- Choosing the most appropriate method for solving systems of
equations. - Use letters, boxes, or other symbols to stand for any number, measured quantity, or object in simple situations to demonstrate the beginning concept of a variable and writing formulas.
- Identify and use various indicators of multiplication (parentheses, X, *) and division (/).
- Identify, describe, and extend arithmetic patterns, using concrete materials and tables.
- Use input/output or function box to identify and extend patterns.
- Use and interpret variables and mathematical symbols to write and solve one-step equations.
- Functions describe patterns.
- Functions are relationships or rules that uniquely associate elements of one group to elements of another group.
- In a functional relationship a change in one group causes a change in the other group.
- Functions can be used to represent and solve problems.
- Functions that represent an event can be expressed in different ways.
- Variable
Rational and irrational numbers
- A rational number is a number that can be expressed as a fraction of an integer number:
- Where both the numerator and denominator are integers. (numerator/denominator) (5, 5/1, -6/1, ½, 22/7, 1/3) all are composed of integers.
- The denominator can’t be zero. (5/0)
- Integers, finite decimals, and repeating decimals (.333333) are rational numbers.
- Irrational numbers are real numbers that are only represented by decimals that never terminate (decimals with a long line of different numbers).
- square root of 2, 1.4142135 … never terminate and can't be represented as a simple fraction.
- square root of 3 1.732050807…
- PI is a real number and irrational number 3.141592653589 … Can’t be written as a simple fraction.
- ( √2)2 or the square root of 2 times the square root of 2. Is 2 a rationale number (2/1).
Ratio and proportion
- Ratio is the relationship of one thing to another represented by their numerical values, numbers.
- Ratio are communicated with words (written and oral) in fractional form (½, 3/6) , and as quantities separated with a colon 1:2, 3:6.
- Fraction is a ratio as it is the relationship of a part to a whole. The numerator is a fraction part of the whole, and the denominator (downstairs number) is the number of parts in the whole.
- Ratio is found by dividing one number by the number to which it is being compared.
- Ratios are used to compare two quantities with the same unit.
- Ratios result in treating numbers as a relationship to each other to form new numbers.
- For equivalence a ratio must be kept constant.
- Rate is a kind of ratio. A comparison of two numbers with different units.
- Measurement of distance and time - miles per hour. A value for an amount of something. Gas - price per gallon, Apples - pounds per dollar. Measurement of change of a part’s relationship to a whole - birth rate as part of population growth
- Rates and ratios can be used to make predictions.
- Ratio tables can be used to make predictions.
- Percentage is a ratio as a part of one hundred.
- Proportion is an equation or statement with two equal ratios. Written as 3/4=6/8 and 8:12::2:3.
- Cross products can be used to determine if two proportions are equivalent.
- Ratios and proportions result in forming new ways to represent rational amounts and proving that many forms are equivalent even though they don't look alike.
Advanced concepts
Educator notes
Equality, equals, & equal arm balance
Possible outcomes
- Represent patterns and relationships in a variety of formats and use these representations to predict unknown values and justify solutions.
- Interpret graphs that represent linear and non-linear data and the relationship of the variables.
- Construct and analyze tables and graphs to describe how change in one variable affects a related variable.
- Match visual characteristics of slope with its numerical value by comparing vertical change with horizontal change of two variables.
- Solve problems involving the intersection of two lines on a graph
- Solve and verify simple linear equations algebraically and with representations.
- Create and solve problems, using linear equations.
- Correctly graph a set of equations on the same Cartesian coordinate system
- 1. Set up and label a coordinate system
- 2. Select an appropriate scale
- 3. Represent given equation graphically, accurately and neatly
- 4. Plot points accurately and neatly
- 5. Describe the relationship between the variables
- Identify the solution set from the graph as an ordered pair and explain clearly parallel, identical and intersecting lines
- Solve systems of linear equations using substitution.
- Solve systems of linear equations using elimination/linear combination.
- Identify the most appropriate method for solving a system.
Solve application problems involving a system of linear equations.
- Accurately identify the variables before setting up the problem and translating the word problem into an equation.
- Correctly translate word problems into appropriate equations.
- Solve the system accurately using the most appropriate method and labeling the answer using the correct units.
- Solve problems involving equations and inequalities.
- Use appropriate methods to solve linear and quadratic equations.
- Solve problems involving systems of two equations, and systems of two or more inequalities.
- Solve equations using graphing, substitution, elimination, or matrices (x + y = 7, x - y = 1) and (2x - y > 4, x + 3y <= 9)
Simultaneous linear equations scoring guide
- Inconsistently solve problems involving two or more equations.
- Solve problems with two or more equations by elimination and graphing
- Solve problems with two or more equations by elimination, graphing, substitution, and matrices as well as create equations from graphs.
- Solve problems with two or more inequalities by creating equations when given a graph.
Polynomials
Look like:
- 2xy2 +2x + 4 Which has three terms.
- Polynomials can have zero, one, or more
- constants (3, 1/2, -4),
- variables (x, y, z), and
- exponents (x2, y2 x0), never x-2
- they can be combined with +,-,*,/ operations.
- However, never by division with a variable (2/x)
- They can have one or more terms, but never infinite.
- 5 can be a polynomial because one term is OK.
- x/2 is, because division by a constant is ok.
- √2 is, because it is a constant 1.4142...
- √x is not, because it would have an exponent of 1/2
- 1/x, no ... remember never by division with a variable
- Because of these rules polynomials are easy to manipulate.
- If you add polynomials you get a polynomial
- If you multiply polynomials you get a polynomial.
- If you divide polynomials you may not get a polynomial.
- Standard Form for a polynomial is written with the terms in order by their degree, with the highest degree first (2x2 + 4xy + 8). Degree determined by the exponent (0 is constant (3), 1 is linear (x), 2 is quadratic (x2), 3 is cubic (x3), 4 is quartic (x4))
- Monomial has 1 term, binomial has 2 terms, trinomial has three terms. (think monocycle, bicycle, tricycle) Also quadrinomial.
Logarithms
Common Logarithms have a base of ten. It is the log button on calculators.
- log (100) means.
- log 10(100)=2; Meaning 102= 100
- log 10(1000)=3; Meaning 103= 1000
Natural logarithms use 2.71828. Euler's Number (e) as the base. It is the ln button on a calculator.
- It is how many times e is multiplied to get a specified number.
- Most used logs are common, natural, and base two. Graph for all three.

Data Analysis and Probability
Misconceptions and concepts
Data Analysis
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Data is only related to one thing. Height is related to each person.
Beginning concepts (preschool - 7 years)
- Number values can be attached to objects, ideas, and their associated properties.
- Information about objects can be collected, compared, interpreted, organized, displayed, and used to explain something about the objects.
- Data can be arranged in different ways.
- Organization of data can help interpretation (diagrams, Venn diagrams, tables, charts, ...)
- Samples can be used to make predictions.
- Range of data is the spread or difference between the least and most set of quantities (smallest and largest quantities) Range is affect most by an extreme quantity.
- Mean (arithmetic mean or average) is the sum of the value of each item divided by the number of items.
- Mode is the item represented the most in a set of data.
- Median is the middle set of data.
- Table is an organized set of data.
- Bar graphs visually represent categorical data.
Literate concepts (middle level to adult)
- Data can be arranged in different ways and forms.
- Some representations communicate better than others.
- Organization of data can help communicate, analyze, and interpret it. (diagrams, Venn diagrams, tables, charts, tables, graphs, ...)
- Different data measurements may be appropriate to describe different sets of data.
- Bar graphs are used with categorical data.
- Samples of a data set can be used to make predictions of a total set.
- Range of data is the spread or difference between the least and most set of quantities (smallest and largest quantities) Range is affect most by an extreme quantity.
- Mean is the the quotient of the sum of data points divided by the number of data points; (arithmetic mean or average) is the sum of the value of each item divided by the number of items.
- Median is the middle point, or the middle set of data, when all data points or measurements are ordered from smallest to largest.
- Median is the average of the middle points of a sequence of data points arranged by value.
- Median is the value at the midpoint of a frequency distribution such that there is an equal probability of falling above or below it.
- Median is equal to the number of cases plus one divided by 2. It would be the middle value in an odd number set of cases or the mid point between the two middle sets of cases in an even number of cases.
- Mode is the item represented the most in a set of data.
- Measure of central tendency includes average, mean, mode, median...
- Table
- Scatter plot is a representation of all data points.
- Stem and leaf plot (display) shows all the data points in a table. It can be used to find mean, median, or mode.
- A boxplot is a rectangle positioned according to the quartiles and median of the data set. Or in some situations the mean and range.
- Line graph - See fact sheet
- Cluster is a group of data points close together separated by gaps between data.
- Outlier is an isolated data point, or cluster of data, some distance away from the rest of the data.
- Pie chart
- Categorical data - See fact sheet
- Continuous data - See fact sheet
- Different scales on a graph creates different impressions of the same data.
- Symmetric, A distribution where one have looks like the other half (mirror images).
- Crowd sourcing can improve the accuracy of predictions. Weight of an ox - Dalton 1906.
- Skewed is a distribution that has a long thin tail stretching in one direction.
- Normal curve of distribution is also know as the Gaussian curve.
Advanced concepts
- Sigma (SD, standard deviation) represents the measure of the amount of variation or dispersion of a set of data values.
Educator notes
Many activities that include data analysis concepts will relate well to communication of mathematics concepts.
Outcomes related to data analysis and communication
Beginning
- Organize concrete objects according to related properties for quantities from least to most.
- Identify properties of objects and events and use them to organize and describe data by quantities: least, most, range, and mid values.
- Collect, record, organize, and interpret data in line plots, tables, charts, and graphs (pie graphs, bar graphs, and pictographs).
- Use pictures or symbols to represent properties of quantity of objects to describe those objects or events by range, least, most ...
- Describe like properties with different values as variables. Such as size of dogs can vary.
- Describe relationships with other properties and variables.
- Draw valid conclusions from data displayed in tables, tables, charts, and graphs (pie graphs, bar graphs, and pictographs).
Literate
- Understand the methods and ethics associated with collecting, analyzing, visualizing, and communicating data used to explain the world and world events.
- Collect, construct, and interpret data displays and compute mean, median, and mode.
- Make predictions from data and explain reasoning and informal measures of central tendency.
- Analyze statistical claims and design experiments, and they may use simulations to model real-world situations.
- Some understanding of sampling and make predictions based on experiments or data.
- Comfortable using various graphs to represent different types of data in different situations.
- Represent patterns and relationships in a variety of formats and use these representations to predict unknown values and justify solutions.
- Interpret graphs that represent linear and non-linear data and the relationship of the variables.
- Construct and analyze tables and graphs to describe how change in one variable affects a related variable.
- Match visual characteristics of slope with its numerical value by comparing vertical change with horizontal change of two variables.
- Solve problems involving the intersection of two lines on a graph
- Solve and verify simple linear equations algebraically and with representations.
- Create and solve problems, using linear equations.
- Describe a graph by identifying intercepts, slopes, maximum, minimum, increasing, decreasing, parallel, and perpendicular.
- Use families of curves to describe the effect of changing coefficients of an equation.
Graph a set of data on a Cartesian coordinate system - See fact sheet
- Set up and label a coordinate system
- Select an appropriate scale
- Represent given equation graphically, accurately and neatly
- Plot points accurately and neatly
- Describe the relationship between the variables
- Identify the solution set from the graph as an ordered pair and explain clearly parallel, identical and intersecting lines
Make stem and leaf plot
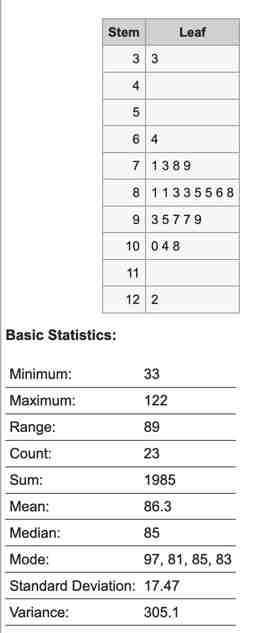
Source: Stem-and-Leaf Plotter
Probability
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- I can cause a certain tile to be selected. (think real hard, pick a certain way...).
- One object (event) always gets chosen more often.
- It is magic.
- Learners will select the second statement, with multiple possibilities, as more probable (conjunction fallacy).
- A survey was given to a representative sample of students in grades 1-12. J. T. was included in the sample and selected by chance. Which of the following is more probable? 1) J. T. missed five days or more of school. 2) J. T. missed five days or more of school and is below sixth grade.
Beginning concepts (preschool - 7 years)
- An event has a set of outcomes. The smallest set of outcomes is the empty set or impossibility.
- Predictions are derived from possibilities.
- A prediction about a set (population) can be made from one or more samples of the set.
- Some possibilities have a better chance of occurring than others.
- Some possibilities are not likely to happen.
- Some possibilities are impossible to happen.
- Events are impossible, possible, or certain.
- Probability is how likely an outcome is to occur.
- A fair game is one in which every player has an equal opportunity to be successful.
- A tree diagram can be used to identify all outcomes of events.
- Each selection increases the possibility of selecting all possibilities at least once.
- Accuracy of prediction may be increased with more trials.
Literate concepts (middle level to adult)
- An event has a set of outcomes. The smallest set of outcomes is the empty set or impossibility.
- Events can be impossible, possible, or certain.
- Probability is how likely an outcome is to occur.
- The probability of an outcome is the number of specific outcomes out of the total number of all possible outcomes of one event.
- Probability can be used to make predictions.
- Probability can be determined theoretically (Use reasoning to find the total possible outcomes, the total of each specific outcome, and the proportion of the specific to the total).
- Probability can be determined experimentally (Experimentally collect data for each specific outcome and use it to calculate the proportion of the specific to the total).
- Probabilities can be written in the form of a fraction, decimal, and percent.
- Probability is between 0 and 1.
- A fair game is one where all participants have equal chance of success.
- A tree diagram can be used to identify all outcomes of events.
- Conjunction rule: the probability of two events occurring (in conjunction) is always less than or equal to the probability of either one occurring alone.
- The law of large numbers can't predict one flip, but can predict the average of 00 flips. Example batting or shooting average for a season v. for a game. The origin of the law of large numbers stems from the 16th century Italian mathematician Gerolamo Cardano, who stated that the accuracy of empirical statistics tends to improve with the number of trials.
- Statistical probability varies from 0 to 1.0. With the probability of a head to come as a result of a coin flip being .5.
- Ronald Fisher (1925) advanced the idea of statistical hypothesis testing, which he called tests of significance which he suggested a probability of one in twenty or 0.05 as a convenient cutoff level to reject the null hypothesis.
Advanced concepts
- Chirality is the property of a structure that its mirror image can not be superimposed on each other. Example. Left hand is chiral to a right hand. Left hand image can not be superimposed on the image of a right hand. Used mostly to describe molecules, atoms, ions, and other particles.
Educator notes
Children can accurately predict relative probabilities with the use of perception for probability devices that are scaled (spinners with different colored sections of different areas, different amounts of colored objects in a container).
Conduct experiments or simulations to demonstrate experimental probability, theoretical probability and relative frequency.
Learners will select the second statement as more probable (conjunction fallacy).
- A survey was given to a representative sample of learners in grades 1-12. J. T. was included in the sample and selected by chance. Which of the following is more probable? 1) J. T. missed five days or more of school. 2) J. T. missed five days or more of school and is below sixth grade.
Probability [(JT in 5 grade) & (JT less than 6g)] < or = probability (JT in 5 grade)
Learners who make these errors may not understand probability, may use intuition to connect what seems more normal, not understand intersection, inclusion, or subsets. Venn diagrams can provide learning and instructional support to represent these ideas.

Geometry
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Shapes are defined by their outline not properties.
- Measurement is counting.
Beginning concepts (preschool - 7 years)
- Shapes are identified by their properties.
- Shapes are categorized by their properties. (classification)
- Length is a property.
- The length of a shape can be compared.
- All objects have properties or attributes that can be measured.
- Measurement can be with standard and non standard units.
- Standard units of measurement make it easier to communicate measurements.
- Properties which can be measured are: linear, area, capacity, volume, weight, mass, time
- Standard units include linear (inches, feet, miles; cm, m) capacity (ml, l, cup, pint, quart, gallon) time (second, minute, day, week, month, season, year) weight (gram, kilogram, pound)
Literate concepts (middle level to adult)
Geometry originates from Greek ge or gaia meaning earth or land and metria meaning measuring, or measurement of earth or land. Today geometry’s big ideas include the study of spatial properties and relations of points, lines, surfaces, solids, and higher dimensional quantities. Their shapes, variables or invariables, definitions, & proofs.
- Measure is the action to find the size, amount, or degree of something. Usually an object, set of objects, or quantity of matter. Usually by using an instrument or device that compares the unknown to standard units.
- We measure with different accuracies depending on the selection and use of a measurement system, units, tools, and purpose of the measurement.
- Measuring is a process that starts with the identification of something to measure - a property of an object or event, then a selection of a measuring system and appropriate unit (standard or non standard), and finally a process to iterate the unit across the unknown object or event to be measured.
- Area is the surface space of a two-dimensional space measured in square measurements.
- Angle is made where two lines intersect.
- Circle is a two dimensional closed figure with every point being equal distance from its center.
- Circle properties include: circumference, diameter, radius, sector, chord, area, and infinite lines of symmetry
- Congruence is when two figures have the same shape and size.
- Coordinate system is a spatial reference system that uses vertical and horizontal references from a point of origin.
- Line is
- A line has different properties (line, line segments, ray)
- Patterns can be described mathematically.
- Parallel lines are lines in the same plane that do not intersect.
- Perimeter is the distance around a shape measured in linear measurements.
- Perpendicular lines intersect so they form a right angles or 90 degree angle. Can be made on a piece of paper holding the points on either end of the line together and folding at the mid point.
- PI is the relationship between the diameter of a circle and its circumference.
- Pi is a real number and irrational number 3.141592653589 …
Meaning it can’t be written as a simple fraction with a numerator and denominator with both being integers.
- 22/7 is not PI. It is an approximation of PI (3.14285714) and a rational number.
- 355/113 Is also an approximation of PI (3.14159292) however, closer. It is also a rational number.
- Nilakantha (an Indian mathematician who lived in the years 1444–1544). Discovered this recursive pattern 3 + 4(2×3×4) − 4(4×5×6) + 4(6×7×8) − 4(8×9×10) + … to represent PI as π = 3.141592653340544
- Plane is a flat surface such that if a straight line is draw from from on point on the line to another, the line would be entirely on the surface.
- Point is a place in space that has a location, but no size. It is impossible to draw, because if it is, then it has size.
- Polar coordinate system is a spatial reference system that uses and angle and distance for reference from a point of origin.
- Polygon is a plane figure whose sides are line segments. They can be convex or non convex. Regular polygons have angles and sides all of equal measure.
- Relative position is used to locate objects in space (directions). Use vocabulary involving important prepositions: in, on, under, inside, between, upon, from, outside, above, and so on.
- Spatial relationships and Geometric patterns can be found in our everyday world.
- Spatial representations can be shown with models, diagrams, ... (geoboards, visual representation).
- Symmetry
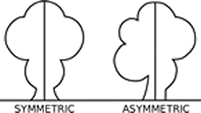
- Symmetry or line symmetry is an identical relationship on two sides of a line drawn through a figure or parts of a figure. A figure has line symmetry if a part can be flipped about a line so both parts coincides. A mirror can be used to illustrate symmetry if placing the mirror on the line of symmetry the reflection is the same as the figure in front of the mirror. Symmetric parts are unchanged when reflected, rotated, or scaled.
- Tessellation is a 2-dimensional pattern made from plane figures that fit together to fill the plane, leaving no spaces.
- Triangle is a two dimensional (plane) closed figure with three straight sides and three angles.
- There are three kinds based on the length of their sides.
- Equilateral - three equal length sides.
- Isosceles - two equal length sides.
- Scalene - all sides are different lengths.
- Perpendicular bisectors can be made by joining the vertices and folding between them.
- Midpoint can be found by folding all three perpendicular bisectors and finding their union, where they cross.
- Trigonometry is the study of triangles and the relations of their sides and angles.
- There are three kinds based on the length of their sides.
- Two-dimensional geometric figures include: circle, square, triangle, rectangle, polygon, ...
- Volume is the amount of space an object occupies.
- Pythagorean theorem a2 + b2 = c2
Advanced concepts
Educator notes
See also Teacher resources
The Pythagorean theorem was known long before Pythagoras, but he may well have been the first to prove it. Chinese knew of it 600 years earlier than Pythagoras.
Measuring the hypotenuse of a right triangle led to the idea of square roots as a right triangle with two sides, each 1 unit will make the hypotenuse the square root of two. Which created a problem of how to solve for it. 1 2/5 , not good enough, 1 41/100 closer, 1 207/500 closer, but can't really get there. Which led to irrational numbers.

Measurement
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Units change in their value.
- Other people will know what unit I reference. (No understanding of a standard unit).
- Any unit is okay.
- Move unit and count. (No understanding of accuracy needed in placing unit(s) of measurement.
- It's possible for a measurement to be perfectly accurate.
Beginning concepts (preschool - 7 years)
- All objects have properties.
- Properties (attributes) can be measured. You need to identify what (property or attribute) to measure.
- Length is a property.
- The length of a shape can be compared.
- Objects measurements are conserved when they are moved. Moving an object does not change the measurement of its properties or its attributes (length).
- Conservation of number - the number of objects does not change with the position of the objects.
- Conservation of length - length of an object does not change when its position is changed or its shape is altered by bending.
- Measurement can be with standard and non standard units.
- Standard units of measurement make it easier to communicate measurements.
- Properties which can be measured are: linear, area, capacity, volume, weight, mass, time Standard units include linear (inches, feet, miles; cm, m) capacity (ml, l, cup, pint, quart, gallon) time (second, minute, day, week, month, season, year) weight (gram, kilogram, pound)
- Objects can be used to compare other objects.
- We measure an entire length by iterating objects (snap cubes, strings of paper clips, strips of paper, yarn along the entire distance without gaps or overlaps (continuous).
- We can estimate by visualizing a unit (standard or non-standard) compared to what you don't know,like book length is so many (blocks, paper clips, iinches, cm ... ) long.
- Measurement is a way of detecting change.
- Linear measurement is the distance between two points.
- Volume is the measurement of space an object occupies.
- Area measures the surface of an object.
- When the thermometer goes up the temperature is hotter.
- Measurement helps in making better observations.
- Scales measure weight.
- Measuring cups measure capacity
- Measurements can be compared.
- Measurement is used in everyday life (recipes, plans, designing, building)
- Time is the measurement of years divided into: seconds, minutes, hours, days, weeks, months, seasons, decades, centuries.
- Mathematics can be used to solve problems with time.
- Time is communicated in standard units.
- The duration of an event from the beginning to the end is measured in time.
- Time represents past, present, and future events.
- There are tools of measurement that hep us make better measurements: clock, calendar, balance, ruler, ...
- Units can be partitioned into fractional amounts smaller than the standard or nonstandard unit.
- It is necessary to recognized what numbers on a tool represent for what is being counted. Minutes, hours, seconds on a clock or inches or centimeters on rulers. Cups, pound, kilograms, liters, ml, ...
Literate concepts (middle level to adult)
- Measure is the action to find the size, amount, or degree of something. Usually an object, set of objects, or quantity of matter. Usually by using an instrument or device that compares the unknown to standard units.
- We measure with different accuracies depending on the selection and use of a measurement system, units, tools, and purpose of the measurement.
- Measuring is a process that starts with the identification of something to measure - a property of an object or event, then a selection of a measuring system and appropriate unit (standard or non standard), and finally a process to iterate the unit across the unknown object or event to be measured.
- Measurements are conserved.
- Conservation of volume - volume of an object or substance does not change when the position and shape of the object or substance change position.
- Conservation of mass - mass of an object or substance does not change when the position or shape of the object or substance changes.
- Conservation of area - area of a surface does not change when the position of the surface changes position.
- Properties and change of properties can be quantified.
- All measurement is relative to a unit, usually a standard unit.
- Scale is proportional.
- Measurement helps in making better and more accurate observations.
- Quantitative estimates of familiar lengths, weights, and time intervals can be confirmed by measurement.
- Rulers are used to measure linear measurement.
- Scales measure mass and weight.
- Measuring cups measure volume and capacity.
- Measurement is used in everyday life (recipes, plans, designing, building).
- Rate is based on time.
- Standard units help communicate
measurements better than non standard. They include:
- Linear measurement standard units are cm, m, km, inch, foot, yard, mile
- Volume- standard units include liter, ml, cup, pint, quart, gallon
- Time - measure in units of seconds, minutes, hours, days, weeks, months, years, decades, centuries. Time is used to order events. Twenty-four hours in a day, about 30 days in a month, 365 days in a year, 52 weeks in a year, 12 months in a year. Calendar is used to measure time. Clocks are used to measure time. Clocks can be analog and digital. A day is divided into daytime and nighttime. Time is determined by Earth's movement. Time is cyclic (seasons, days of weeks, months).
- Temperature measures hot and cold. Degrees in Celsius and Fahrenheit are standard units of temperature
- Mass - standard units are g, kg, pounds, ounces, tons
- Units can be used as additive. They can be composed and decomposed. (ten can be used as a composition of six units and four units or ten units of one group).
- Money is represented in increments of .01, .05, .1, .25, .5, 1.00, 2.00, 5.00 10.00, 20.00, 50.00, 100.00 (beats me from here)
- Interest is a percentage paid for the use of money.
- All measurement has error. because
- All measurement is approximate. The choice of unit in relation to the object determines the precision.
- Measurement tools
- Each measurement tool has a conventional zero point, but any point can be used as an unconventinal zero point.
- To understand how a tool works we need to know what numbers represent on different measurement tools. (rulers, clock, protractor) and what is counted.
- Using measuring tools are more efficient than using multiple single units.
- The same property or attribute of an object can be measured with different units, and the resulting measurements are inversely proportional to the size of the unit.
- Different standard units can be converted to other units of the same type of measurement.
- Measures are transitive. ( if A > B and B > C, then A > C).
- All measurement is inaccurate and therefore an estimation.
- We can estimate measurements by visualizing units of measurement and how they can be iterated across what is to be measured.
- People choose how to estimate by the accuracy required.
- Estimation is an approximate selection of a unit of measurement and the number value used for the actual measurement (... .001, .01, .1, 0, 1, 10, 100, 1ooo, ...).
Advanced concepts
- Scale is a proportional relationship of characteristics, properties, or relationships within a system as its dimensions are increased or decreased.
- Rate involves a measure of change for a part relative to a whole (birth rate as part of population growth and comparing one measured quantity to another measured quantity (km per hour).
Educator notes
See also

Number value & Basic operations
Whole numbers, Place value, fractions, decimals, percent, integers
Whole number value
Misconceptions and concept
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Number words are like a rhyme onetwothreefourfivesix...
- Counting is saying the number words onetwothreefourfivesix...
- Counting is saying the number words and pointing.
- When multipling by ten add a zero.
- You can't subtract a bigger number froma smaller number.
- Addition and multiplication make bigger numbers.
- Subtraction and division make smaller numbers.
- You always divide the larger number by the smaller number.
- Improper fractions should always be written as a mixed number.
- The number you say first when counting is always less. (2 dozen eggs, 8 eggs, 12 eggs)
- The longer the number the bigger the number.
Beginning concepts (preschool - 7 years)
- Certain words are used for counting.
- One-to-one correspondence
- Cardinality
- Conservation of number
- Hierarchical inclusion for counting
- Addends as cardinal values
- Counting on
- Ordinality
- Total hierarchical inclusion
- Count back
Literate concepts (middle level to adult)
- Number notation
- Number relationships
- Simple one-to-one relationships
- One to many relationships
- Hierarchical inclusion for number value as addition
- Nominal numbers
- Infinity
Advanced concepts
Educator notes
The development of number sense is outlined in the following:
- Prenumber sense development ( Classification, Counting, Synchrony, One-to-one correspondence, Counting systematically, Subitizing, Conservation of numbers, Number value or Cardinality, Zero, & numbers beyond 10)
- Number sense development (Cardinality, Ordinality, Number notation, Number relationships, Simple one-to-one relationships, One to many relationships, Hierarchical inclusion for counting, Hierarchical inclusion for number value as addition, Number value and operations, Zero, Beyond ten, Nominal numbers, Infinity)
- Counting (Includes same ideas as in prenumber sense and number sense development in one document)
- Place value development
- Activities
- Vocabulary
- Development of conservation & reasoning tasks & notes & notes
Place value
Misconceptions and concept
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Each number is like a unique name for a value.
- There is no pattern for numer name and the value it represents.
Beginning concepts (preschool - 7 years)
- Ten is a big number.
- Ten is a bigger number than 1, 2, 3, ... 9.
- Ten is less than 11, 12, ....
- Objects can be grouped by tens.
- Groups of ten are equivalent.
- Grouping by tens makes it easier to count.
- Objects can be grouped into tens and leftovers.
- Ten is a group of ten ones.
- Objects in groups of ten can be combined by skip counting by tens.
- Counting by tens is helpful.
- Counting by tens is like counting by ones with zeros.
- Objects can be grouped into tens when thinking of number value and to solve problems. (significance of ten)
- Numbers can be grouped as ten and more.
Literate concepts (middle level to adult)
- Unitize - groups of ten are simultaneously both: equal groups of ten and the equivalent number of units or ones. For example thirty is simultaneously three equal groups of ten and thirty ones. In 30 the three means three groups of ten or thirty ones (plus zero additional ones represented by the zero). In 32 the three means three groups of ten or thirty ones plus two additional ones represented by the two.
- Place value unitizes by tens, hundreds, thousands, ...
- Numbers can be located as nearest to a selected number value (measuring, estimation, rounding).
- Rounding is an approximate estimation to a selected value (... .001, .01, .1, 0, 1, 10, 100, 1ooo, ...).
- Rounding is not a property of numbers but a property of a system of numbers used to represent them.
- Ten has a significant role in our base ten number system. Ten, hundred, and thousand are important multiples of this number system.
- A number system is a code that uses a set of symbols (numerals) and rules for combining the symbols to represent number values.
- All numbers can be represented with only ten symbols or numerals.
- Ten numbers can represent any unit (ones, tens, hundreds, …).
- Zero has an important function in writing numbers.
- Position of a digit can represent different values.
- The sum of the value of all digits determines the value of a numeral (cardinality) The total value of a numeral is the sum of all digits values in its particular place. A digits value is a function of its number value and it's place value.
- Numbers can be composed and decomposed into different equivalent groups of tens and more (taken apart (decomposed) and put together in different order (composed) or regrouped and written in expanded notation.
- Numbers of groups can be operated on without regard to the value of the group (62 - 41), (60 - 40) can be operated as (6 - 4) and (2 - 1) and write, think, or say 21 without really (multiplying by ten). This thinking about and working with groups is a result of unitizing.
- Addition facts can often use ten as an anchor (32 = 30 +2) for addition and subtraction. This is helpful when adding (27 + 35), (27 + 30) + 5 = (57 + 3) + 2 = 62 both for adding or subtracting to make tens, and adding and subtracting in leaps of ten.
- Place value is exponential: 100,101,102, 103...
(50 = 5 * 101+0*100,
51 = 5 * 101+1*100,
52 = 5 * 101+2*100,
200= 2*102 +0*101 + 0*100,
201=2*102+0*101 + 1*100,
234=2*102+ 3*101+4*100) - Decimals as exponential: 10-1,10-2, 10-3
- Unitizing place values of decimal numbers, less than and greater than one, as an exponential progressions.
- Hindus are credited with the invention of a place value system.
- The Arabs are credited with applying and spreading its use.
- Translations of Fibonacci's work introduced it to Europe.
Fractions
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Fractions are pieces of a whole, that don't have to be equal sizes.
- Fractions are pieces of things.
- All fractions are smaller than one.
- The bigger the denominator the bigger the fraction.
- Fractions are added by adding the numerator with the numerator and denominator with the denominator.
Beginning concepts (preschool - 7 years)
- Fractions are equal parts of a whole or a equal subgroups of a group.
Literate concepts (middle level to adult)
- Fraction is equal parts of a whole (one).
- Fractions are part/whole relations.
- Fraction is equal parts of a set or group (of wholes or fractional parts) that is considered one whole.
- Human beings constructed fractions to deal with fair sharing situations.
- Fractional parts must be equivalent and they must be equivalent in relationship to the whole.
- The whole matters.
- Fractions are relations.
- To compare fractions they must be compared with the same whole.
- Fractional parts don't need to be congruent to be equivalent.
- Fractional parts can be compared with - compensation. Move a part from one place to another, as long as every move or loss has an equal gain or opposite move.
- Fractions are divisions (
- One-half. is one divided into two
- Three pizza's divided by four people. Each person gets 3/4 of a pizza. 3 divided by 4 = 3/4).
- Multiplication is connected to fractions (3/4 = 3 * 1/4).
- Numerators are the upstairs numbers and denominators are the downstairs numbers.
- If numerators are common, then denominators matter when comparing (3/5 > 3/7 > 3/8).
- If denominators are common, only the numerators matter when comparing (1/3 < 2/3).
- The bigger the denominator the smaller the piece (1/2 > 1/4).
- Equivalent fractions are equal representations of the same whole, part, group, or set (1/2 = 2/4 = 3/6 = 5/10).
- Equivalent fractions represent different ways of describing the same amount using different sized fractional parts (1/2 = 3/6 = 4/8 = 50/100).
- Fractions can represent parts and wholes.
- Whole numbers can be represented as fractions: 2/2, 3/3, 4/1 ...
- Fractional names tell how many parts of equal size are needed to make a whole (fourths means four equal parts make a whole).
- The more parts needed to make a whole, the smaller the parts (four parts are bigger than eight parts of the same whole).
- The numerator tells - how many parts are represented and the denominator tells - the kind or number of parts the numerator counts.
- Simple fraction - is a fraction where both the numerator and denominator are integers (whole numbers). Also known as a quotient of two integers.
- Zero parts can never make a whole. Therefore, a fraction can never have a denominator of zero.
- Fractions can be added, subtracted, multiplied, and divided.
- Fractions, decimals, percents have a unique relationship.
- Interest is a percentage usually related to the use of money (loan rate, sale discount).
Advanced concepts
Educator notes
A good assessment strategy is to ask how a fraction compares to land mark numbers: such as near 1, 1/2, 1/4 ... Is 3/5 closer to 1 or 1/2?
Historically the first evidence of recorded fractions were used in the context of division problems which didn't have whole number solutions. Written such as 2/3 meaning two to divide among three. Maybe the peasants grain was to be divided into three: one for the king, priest, & the peasant.
However, before fractions as mathematical numbers people probably called had names for parts and maybe equal part such as half. All fractional numbers use whole numeral names for the denominator, except half. This may indicate that people understood halves as equal parts before numbers were well developed into a number system. Make a list of synonyms for half is small ... (half, twin) ... compared to a fractional part without specific quantity (part, piece, portion, portion, share, slice, chunk, fraction, section, member, region, territory, bit, hunk, morsel, crumb, shred, cut, ) or fractional parts with a quantity other than half (thirds ... ? , fourths ... ?, fifths ...) (Also vocabulary for numbers)
Decimals
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Misconception .9 doesn’t equal 1. Recognize 1/3 = .3 & 2/3 = .6. but not .9 = 1.0
Beginning concepts (preschool - 7 years)
- Money is a decimal number
Literate concepts (middle level to adult)
- Decimals can represent fractions
- Decimals can represent percents
- Decimals can represent ratios
- Decimals represent division
- Decimals are based on place value
- Fractions, decimals, percent have a unique relationship.
- Whenever a fraction has a denominator of ten the numerator represents tenths. 3/10 = .3, 53/10= 5.3…
- All 1/2 fractions are equal to .5
- Out place value is a base ten.
- Base ten is infinite in both directions.
- Decimal point is read as and when reading decimal numbers.
- Decimal point locates the units position.
- Adding decimals is like adding fractions with common denominators
- Digits of numbers must be added according to their place values.
- Digits of numbers must be subtracted according to their place values.
- Dividing by 10, 100, 1000, gives an answer that has as many digits to the right of the decimal as zeros on the number you are dividing. This happens because you are dividing by factors of ten.
- Multiplying by ten is like moving the decimal one place to make the number larger.
- Base ten is infinite both for number values that increase and number values that decrease.
Advanced concepts
- Decimals either end in zero or repeat as nonterminating decimals or rational numbers.
Example: place these numbers on number line 1, 2/3, .5, .3 , 1 1/2, 2, .6 , 1/2, .9, 1.1, 1/3 Misconception .9 doesn’t equal 1. Recognize 1/3 = .3 & 2/3 = .6. but not .9 = 1.0
Educator notes
Percent
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Percent is a grade given by teachers.
Beginning concepts (preschool - 7 years)
- Percent is part of 100.
Literate concepts (middle level to adult)
- Percent represents hundredths.
- Percent is a relationship of hundredths to one.
- It’s helpful to know and use landmark values: 1%, 10%, 25%, & 50%.
- Fractions, decimals, and percents can be changed back and forth to make problems easier to solve. (1/2, .5, .50, 50%; 10%, .1, .10, 1/10; 1/4, .25, 25%;…)
- Percents are used to make comparisons, which are often used to make decisions.
- Percent can be compared visually as fractional parts, ratios, and percents.
- Fractions, decimals, percent have a unique relationship.
- Percent provides a numerical value to classify probability as: impossible, unlikely, likely, certain.
Advanced concepts
Educator notes
Integers
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
Beginning concepts (preschool - 7 years)
Literate concepts (middle level to adult)
- Integers are whole numbers. 1, 2, 3, 4, … and their negative counterparts. -1, -2, -3, -4, …
- Positive and negative numbers can be used together to describe quantities which have opposite directions or values. Temperature - above and below zero. Elevation above and below sealevel. Credits and debits. Positive and negative electrical charges.
Operations (+, -, *, /)
Misconceptions and concepts
Computational estimation
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Estimation is guessing.
- Since estimation is guessing any estimation is valid.
Beginning Concepts
- Numbers can be taken apart and put together in a variety of ways.
- Estimation can be done by replacing or substituting difficult numbers with close or nice numbers and worked with mentally.
- There is no right way to estimate or compute mentally.
- Estimation is used not only for estimation but also when we use mental calculation, paper - pencil calculation, a computer, and a calculator.
Literate concepts (middle level to adult)
- Some mental computation starts with the large digits and works toward the smaller (left to right). Paper and pencil computation is digit oriented and right handed.
- Rounding is not a property of numbers but a property of a system of numbers used to represent them.
- Rounding is an approximate estimation to a selected value (... .001, .01, .1, 0, 1, 10, 100, 1ooo, ...).
- Estimation accuracy depends on the situation.
Addition and subtraction
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Addition makes more
- Subtraction makes less
Beginning concepts (preschool - 7 years)
Operation of + & -
- There are four ways to apply addition and subtraction
- Combination of number values
- Separation of number values
- Part-part-whole relationships of number values
- Comparing or equalizing number values
Whole Numbers
- Different values of objects can be recognized by a pattern of their position (subitize).
- One more is addition.
- One less is subtraction.
- Two more is addition.
- Two less is subtraction.
- Can add by counting two separate sets of objects, sliding them together into one group, and then count the new group to find how many altogether.
- Two different groups of objects can be added by counting on from the total number in one group.
- Dice can be added by subitizing the first die and counting on.
- How many objects are left in a set of objects can be found by counting back from the total number in an initial group.
- Numbers can be decomposed into smaller groups (addends) and added together in different orders (commute them and compose them) to find the sums.
- Numbers greater than 20 can be added and subtracted by working left to right - decomposing into tens and ones, adding or subtracting tens, then adding or subtracting ones, and then adding or subtracting the tens and ones.
Literate concepts (middle level to adult)
Operation of + & - & (whole, fractions & decimals)
- Addition is the joining of groups (sets).
- Addition can be used to solve joining problems.
- Addition can be used to solve separation problems.
- Addition can be used to solve part - part - whole problems.
- Addition can be used to solve comparison or equivalent problems.
- Subtraction is separation of a set from another set.
- Subtraction is the removal of a group.
- Subtraction is the joining of groups.
- Subtraction can be used to solve part-part-whole problems.
- Subtraction can be used to solve comparison and equalization problems.
- Subtraction is how much is left.
- Subtraction is how much is missing.
- Subtraction is how much more.
- A number can be represented as a difference with different groups of numbers (subtrahends and minuends)
- Addition and subtraction are related.
- Numbers can be operated on with addition and subtraction in different groups of numbers.
- Addition has the commutative property (3+4) = (4+3). The operation or addition has the same value regardless of the order in which the numbers are added. Or if the values commute or change order the addition operation will result in the same sum.
- Addition has the associative property, the sum of a set of numbers is independent of how they are grouped or associated. (1 + 2) + 3 = 1 + (2 + 3).
- Addition has the identity property for 0, zero added to any number is the value of any number, or the number itself.
- Knowing the addition facts of ten helps to use ten as an anchor for addition and subtraction.
- Addition, subtraction, and comparing operations can be thought of as measurement or using a ruler.
- One more and one less is the value before and after a counting sequence.
- Two more and two less is the second value before and after a counting sequence.
- All numbers in a counting sequence can be thought of a distances relative to the amounts being added or subtracted.
- Two separate sets of objects can be added together by counting each set, sliding them together into one group, and then counting the new group to find how many altogether.
- The total number of objects in two separate sets of objects can be found by using the value of one set and counting on from that total number.
- The total number of objects left in a set of objects can be found by counting back from the total number in the initial group.
- Numbers can be added by decomposing numbers into smaller addends, commuting them and composing them with the different numbers. Example - two die with a roll of sixes, decompose them into 5, 5, 1, 1, commute and compose them like 5 + 5 = 10; 10 + 2 = 12.
- Values greater than 20 can be added or subtracted from left to right by decomposing into tens and ones, adding or subtracting tens, then adding or subtracting ones, and then adding or subtracting the tens and ones. For example: 46 + 23 by deconstructing 46 and 23 into 40 + 6 and 20 + 3, then adding the 40 and 20 and then the 6 and 3 and then the 60 and the 9 getting 69.
- Values greater than 20 can be added or subtracted from left to right by starting with an initial number: 46, deconstruct a second 23 to 20 + 3. Then add on from: 46 + 20 to get 66 and then add on the 3 to get 69.
- All addition and subtraction must account for the place value of each number as it is composed or decomposed to arrive at a sum or difference. This can be shown if numbers are decomposed into expanded notation, based on place value, and then each expanded number can be added or subtracted with another number with the same place value. If numbers can't be operated on, then the numbers can be regrouped into different multiples of ten as needed using expanded notation to check for accuracy.
- Addition and subtraction requires numbers be operated on with respect to their place values.
- There are many strategies to add and subtract.
- Making nice numbers (368 + 204 = 368 + 200 + 4 = 568 + 4=572).
- Keeping the whole (71 - 36 = {subtract 1 from both to get} 70 - 35 = 35) (342 - 37 = {add 3 to both to get} 345 - 40).
- Numbers in expanded notation can be added or subtracted if they have the same exponents. If exponents are different, numbers needed to be changed so they do have the same exponent value (place values).
Advanced concepts
- There are no advanced concepts for addition and subtraction as they are operations of arithmetic. Not advanced mathematics.
Educator notes
- Development of addition and subtraction
Multiplication and division
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Multiplication makes more faster.
- Multiplication is just repeated addition.
- Division is just repeated subtraction.
- Division makes a lot less.
- Dividing whole numbers (28 by 14; 2 and comparing the result to dividing 28 by 7; 4) lead learners to believe (conjecture) the smaller the divisor, the larger the quotient. However, dividing numbers by numbers between 0 and 1, such as 1/2, (4 / 1/2; 8) the quotient (8) is larger than the original number (1/2). Of course division with fractions and decimals isn't learned until well after learners probably have created this idea, Therefore, later explorations are important to help correct, this misconception: division always makes things smaller.
Beginning concepts (preschool - 7 years)
Whole Numbers
- Multiplication is a kind of repeated addition.
- Skip counting is repeated addition.
- Multiplication is repeated addition of equal groups.
- Equal subgroups within a collection are connected with multiplication (as repeated addition).
- Associate multiplication and division with repeated groups of equal size.
- Associate division and multiplication as involving the distribution of equal shares or groups.
- Relate multiplication and division as repeated groups of equal amounts or shares.
Literate concepts (middle level to adult)
Whole Numbers
Multiplication
- Multiplication and division are inverse operations.
- What each number in a multiplication or division expression represents as well as the units each represents.
- Factors in multiplication and division can refer to different units. (29 cats with each having 4 legs. 116 is the total number of legs on 29 cats. Can't do with addition. (Need to add and subtract legs with legs and cats with cats. Adding cats and legs isn't reasonable.)
- Multiplication and division problems can be modeled with pictures, diagrams, or concrete materials to illustrate what the factors and the product represent in various contexts. (if there are 112 people traveling by bus and each bus can hold 28 people, how many buses are needed? 112 people put into groups of 28 people, for each bus, will need one bus for each group.) or (If 112 people need to fit among four buses, how many people will need to be on each bus? In this case, 112 people distributed across 4 buses will indicate the number of people on each bus.
- Ways to determine what to do with remainders depend on what is being divided and for the purpose of dividing.
- Multiplication and division are related to rates (3 candy bars for 59 cents each, mph, ).
- Multiplication and division can be used for comparisons (the book weighs 4 times as much as the tablet).
- Multiplication can be used with combinations (the number of outfits possible from 3 shirts and 2 pairs of shorts).
- Dividing numbers between 0 and 1, such as 1/2, result in a quotient larger than the original number. Example: 4 / 1/2; 8 the quotient (8) is larger than the original number (1/2).
- Area models show the relationship of a product to its factors.
- Area models can show multiplication properties.
- Area models can be used with whole numbers, fractions, decimals, and percentages as well as their combinations.
- Properties: such as the commutativity, distributive, and associative can be used to compute multiplication by composing and decomposing. See examples of computation strategies.
- Multiples are products of unitized groups ( a number of groups and units in the group).
- A group of objects can be thought of as both the number of objects and as one group or unit.
- The parts (the number of objects in the group) and the whole (the group) can be considered simultaneously. A bag of six cookies can be both six cookies and one bag of cookies. Three threes = three groups of three. Or a number of groups with a number of objects. This same relationship is necessary to understand place value and exponents. If a person counts equal groups as units, they're probably thinking of multiplication. If they skip count, they're probably thinking of repeated addition.
- Multiplication is counting groups of like sizes and determining how many in all the groups.
- One number (factor) represents the number of groups and the other the number (factor) represents the number of objects in each group, and another is the total (product). [4 (factor) * 3 (factor) = 12 (product)]
- Measurement, area, volume, The product is something different than the factors (square feet is the product of linear feet, cubic cm...). arrays, matrices.
- When the number of groups (factor) is known and how many objects (factor) are in each group is known, then the operation to find the total (product) is multiplication.
- Multiplication names a product in terms of two known factors.
- Digits of numbers must be multiplied according to their place values and for all places.
- Multiplication can be represented as
- The iteration of equal groups
- Measurement: area, volume, ...
- Arrays, matrices, 3-D array
- Trees and branching
- Combinations and Cartesian products
Division
- Division is can be thought of as repeated subtraction
- When either the number of groups or how many objects are in each group is known and the product of these numbers is known, then the operation is unknown as division.
- Fair - sharing or partition problems is when the size of the sets is unknown and the total is partitioned or shared with the known number of groups.
- Division is grouping in equal groups.
- Remainders can be represented by being discarded leaving the smallest whole, forced up to the next whole, round to the nearest whole for an approximate result, or written as a fraction.
- Measurement problem is when the number of sets is unknown and the size of the equal sets is known. The whole is measured into sets of the known size.
- Division names a missing factor in terms of the known factor and the product.
- Digits of numbers must be divided according to their place values.
Properties related to multiplication and division
- One number (factor) represents the number of groups and the other the number (factor) represents the number of objects in each group, and another is the total (product).
- Multiplication and division are related.
- Identity property of multiplication. Multiplication by one.
- Commutative property
- Associative property
- Distributable property
- Factors are divisors of their product
- Primes have only factors of one and the number
- Composites have more factors than one and the number
Fractions and decimals
- Multiplication and division of rational numbers are relations of relations.
Advanced concepts
- Operations can be used in general ways, not only in particular computations.
- Using properties of numbers can help solve problems in unique ways that are more efficient and accurate than using a traditional algorithm.
- Understanding number values and operations help to analyze the accuracy of operations with numbers.
- Problems can be solved by balancing equations [5+7-2=2(5)] or [100/25 = 347-343].
- Algebraic equations include operations and can be solved. (8x+2=50).
- Parenthetical order of operations in equations communicate the order of doinog the operations in an equation. Example (5 * 4) - 15 + 2 and (12 - 2)(3 + 4).
Educator notes
Muhammad ibn Musa al-Khwarizmi invented the present day algorithm in the ninth century. In Latin his name was Algorismus - hence algorithm. Before he invented the algorithm the merchants and intelligentsia used the abacus. The new system with a dust board democratized computation. In the Renaissance in Europe those who knew how to multiply and divide with algorithms were guaranteed a professional career. But today it's different. In 1621 the first slide rule was made. The first mechanical calculator by Pascal in 1642, and the first handheld calculator 1967.
Development of Multiplication and Division Understanding and Strategies

Attitudinal (Dispositions and values)
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
1 (Explanations for people's misconceptions: naive understandings & perceptual responses)
- Believe success is based on luck and not on positive attitudes that shape behavior.
- Believe attitudes are set and not changeable.
The following may be considered for beginning, literate, and advanced levels.
With a depth of understanding and commitment increasing as learners mature and attain additional experience, their depth of understanding and value for each disposition will increase and be exhibited and valued.
The first word or phrase may be considered a concept and what follows is written as outcomes, observable evidence to substantiate them.
Literate Concepts & Outcomes (middle level to adult)
- Acceptant of failure - Considers failure as an occasional part learning and helpful for redirecting.
- Caring, Conscientiousness - Care for others, the natural world, and human-made objects. Caring includes the ways that people individually and collectively participate for the well being of all things for the present and future.
- Cooperative - Works with others for common goals and shares ideas.
- Curious - Asks and answers questions to understand at deeper levels.
- Creative - Imagines ideas that are original or not ordinarily thought
- Disposed to apply knowledge - Ready to think and apply what they know to current related experiences; all ideas from all dimensions (knowledge, processes, attitudes, and perspectives of science).
- Enjoyment - Expresses pleasure in understanding and pursuing understanding.
- Flexibility - Willing to change with new evidence and/ or explanation.
- Grateful - Thankful and appreciative for others contributions.
- Knowledgeable - Knows many generalizations, concepts, and facts; understands inquiry practices; and understands the history, nature, social, personal, and technological perspectives of different subjects.
- Objective - Makes decisions based on facts.
- Open-minded - Tolerates ideas and opinions of others and the importance of carefully considering ideas that may seem disquieting or at odds with what is generally believed and willing to change ideas in light of new evidence.
- Optimistic - Positive, believe people are caring, helpful, and willing to cooperate. Believe solutions are attainable and learning is never complete.
- Passion, zest - Desire to learn, be involved, take action, and believe learning is infinite.
- Persistent, grit - Continues despite obstacles, warnings or setbacks.
- Sensitive - Considers all actions and inactions and the results they might have on all living and nonliving things.
- Skeptical - Doubts, questions, and reconsiders conclusions based on evidence and reasoning.
- Tentative - Hesitant to draw conclusions.
- Reflective - Curious and willingly open-minded to consider new ideas based on evidence and reasoning against previous ideas based on evidence reasoning.
- Responsible - take actions for personal understanding and learning.
- Respect for evidence - Insistent on evidence. Requires evidence to formulate explanations and make decisions and will seek additional evidence and reasons to verify ideas and make decisions.
- Self-control - Choose mastery-oriented behaviors that achieve predictable and reliable outcomes and encourages others to do so also so they may cooperate and be productive.
- Self-efficacy - Believe in their abilities and skills in using different subject practices, processes and knowledge in a useful effective manner to learn and solve problems.
- Sociable, - Values other people and desires to be involved with others to benefit by helping, caring, contributing
- Values communication - Seeks ways to communicate that effectively enable others to accurately conceptualize the ideas wanting to be communicated.
Educator notes
Sugggestions on how to write attitudes, values, disposition, & habits of mind and a list of examples.
Anyone come up with ideas and want to share, let me know...
Classification
Organization, order, & systems (cross-cutting)
Misconceptions and concepts
Coordinate with science
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Things (objects) just have common characteristics or properties for no important or meaningful reason.
- Objects properties are random and have no use in understanding and explaining the world.
- Objects can only be grouped in one way.
- Order exists for no specific benefit (providing understanding or explanation).
- Order is one directional.
- Numbers can't be classified, because they are all different.
- Letters can't be classified, because they are all different.
- Centers on one property, color, shape... to classify when two or more are necessary.
- May believe that since an object was counted once in one group for a property, then that object cant be counted again for another property as doing so would cause a double counting action, which isn't allowed when counting sets, because a one-to-one correspondence means to count each object only once.
- Does not decenter from the use of only one property and simultaneously use two or more properties, when necessary, to classify objects.
Beginning concepts (preschool - 7 years)
Classification & organization (see also science concepts)
- Objects, organisms, events, and systems can be organized into groups with similar properties (classification).
- Classification is one way to organize objects, events, and ideas. (organization)
- Objects have properties.
- Objects are identified by their common properties.
- Objects can be grouped by external properties, color. (3.5 years)
- Objects are classified by there common properties.
- Objects have more than one property. (4.5 years)
- Objects in a group can share some characteristics while differing in others. (4.5 years)
- Objects, organisms, events, ideas, and systems can be organized into groups with similar properties.
- Objects are identified by names.
- Objects with similar properties are the same.
- Objects with different properties are different.
- Objects can have properties that are the same and different, but still be the same (triangles - same shape, different size, color)
- Objects can be grouped (classified) into sets/ groups
- Sets can have cardinality. Cardinality of sets can be the same or different.
- Objects with similar properties that change sequentially can be ordered by that property. See order.
Next classification intermediate concepts
Order
- Order is created by properties that change sequentially. See number sense and cardinality
- Most of the time certain events happen in a similar manner.
- Some events are more likely to happen than others. See probability
- Some events can be predicted more accurately than others.
- Sometimes people aren't sure what will happen because they don't know everything that might be having an effect on the event.
- Often a person can find out about a group of things by studying just a few of them.
System
- Parts are related to a whole.
- A whole is related to its parts.
- Parts are related to parts.
- System is a group of related objects, ideas, and events.
- Most things are made of parts.
- Something may not work if a part is missing.
- When parts are put together they can do things they can't do alone.
Literate concepts (middle level to adult)
Organization & classification Concepts
- Objects, organisms, events, and systems can be organized into groups with similar properties (classification).
- Classification is one way to organize objects, events, and ideas. (organization)
- Objects have properties.
- Objects are identified by their common properties.
- Objects can be grouped by external properties, color. (3.5 years)
- Objects are classified by there common properties.
- Objects have more than one property. (4.5 years)
- Objects in a group can share some characteristics while differing in others. (4.5 years)
- Objects, organisms, events, ideas, and systems can be organized into groups with similar properties.
- Objects are identified by names.
- Objects with similar properties are the same.
- Objects with different properties are different.
- Objects can have properties that are the same and different, but still be the same (triangles - same shape, different size, color)
- Objects can be grouped (classified) into sets/ groups
- Sets can have cardinality. Cardinality of sets can be the same or different.
- Objects with similar properties that change sequentially can be ordered by that property.
- Organization of objects, organisms, events, and systems help people understand similarities and differences that in turn help understand the world.
- Classification is one example of organization.
- Classifications can include class inclusion, a relation between two classes in which all members of one class are included in the other. (8 years) Birds have feathers, there are more birds with black feathers than white. Are there more black feathers than feathers? ... Will answer feathers if have class inclusion.
- Objects are classified by their properties.
- Classification by common properties can create similar groups.
- Objects in a group can share some characteristics while differing in others.
- A group of objects may be sub classified in one or more ways.
- A group of objects may be sub classified as members of an ascending hierarchy. (8 years) A cat is a mammal.
- Descending hierarchy. (9.5 years) Mammals include cats.
- A group or set can be described and classified by processes as well as properties.
- Thinking about things as groups or sets means looking at how every element relates to other members of the group or set.
- Objects may have properties of two different groups or sets.
Order Concepts
- Variables affect the order of events.
- Order is required to understand the world and predict events.
- Probability is the relative certainty or uncertainty that people assign to events happening or not happening in a certain place or time.
- Creating knowledge through observation of different variables influence on objects, organisms, populations, communities, and events helps create better explanatory models
System Concepts
- System is a group of related objects that work together for a particular purpose (machines, organism).
- The parts in a system interact with the other parts to cause the system to work.
- A system may not work if a part is missing, broken, worn out, mismatched, or disconnected.
- Objects can be classified as either natural or of human design,
- Organization of objects, organisms, events, and systems help people understand similarities and differences that in turn help understand the world.
- Sometimes thinking about things as systems improves understanding and sometimes it doesn't.
- System is a group of related objects or components that form a whole.
- Can be concrete objects, groups of objects, processes, or ideas.
- Some systems have boundaries with input and output of resources and feedback.
- Output for one part of a system can be input for another.
- Such feedback is used to control the system.
- Systems are used as units of investigations.
- A system can include processes as well as things.
- Thinking about how a system works means observing and collecting date on each part and how each part interacts with the others.
- Systems can be connected to other systems and thought of as a subsystem.
- Systems may have what appear to be natural boundaries, but are generally arbitrary.
- System ideas are used outside of science. Technology and business use system analysis which looks at systems relationships by their inputs and outputs. Computer programming use these ideas with procedural languages, functions, and object oriented programming.
Advanced concepts
Educator notes
- Classification card set (5 different shapes and colors)
- Conservation assessment tasks
- Classification developmental outcomes for scoring guide or rubric
Communication
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Communication is just something we do to talk to each other.
- Doesn't help to study communication because people are either good at it or not.
- Communication is writing.
- Mathematical ideas can be communicated.
- Mathematical ideas can be communicated in different ways: written narrative, spoken words, pictures, manipulatives, symbols, and movements.
- Combining different ways of communication can make for more efficient or better communication.
- Charts can be used to communcate relationships.
Beginning & literate concepts (preschool - adult) Adapt according to level
- Communication helps us learn from other people.
- Pictures can be used to represent objects and events.
- Communication helps us explain evidence and reasoning to each other.
- Communication requires a message being sent and received.
- Information can be communicated in many different ways each of which have advantages and disadvantages.
- Objects can be described and compared by properties.
- Before and after pictures can be used to represent change.
- Clear communication gives other people information about your discoveries and ideas.
- Explanations are better when specific evidence is provided.
- Communication allows other people to agree or disagree with a person's findings.
- People have always tried to communicate with one another.
- People have invented devices to communicate (paper, ink, radio, telephone, telecommunications, computer disks) Errors can occur when communicating.
- Repeating messages is a way to avoid miscommunication.
- Directions can be written so other people can try procedures.
- Sketches can be used to explain procedures, events, or ideas to the creator and other people.
- Messages can be carried by many different media (light, electricity, sound, objects, glass fibers).
- The ability to code messages has allowed faster communication.
- Numerical data can be used to describe and compare objects and events to the creator and other people.
- Tables, charts, and graphs can be used to represent objects and events.
- Graphs can be used to identify and represent relationships.
- Accurate data keeping and openness are essential to assure an investigator's credibility.
- Graphs can be used to recognize, represent and predict future relationships to the creator and other people.
- Other kinds of tables, matrices, diagrams, webs, symbols, maps can be used to interpret and communicate information.
- Regular and polar coordinates can be used to locate objects.
Educator notes
Most activities can include communication of mathematics concepts.
See examples of outcomes related to communication in data analysis educator notes.
Six ways to communicate mathematically.
- Pictures - Four ways to make 25 cents
- Manipulatives - use of - cubes Writing after Average student height
- Writing - Percentage - Sale problem
- Acting it out - The Door Bell Rang - from the book, The Door Bell Rang by Pat Hutchins
- Symbols - Pigs Go to Dinner - from the book, Pigs Will Be Pigs: Fun with Math and Money. by Amy Axelrod, 1994
- Orally - talk it out.
Connections and perspective
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Mathematics is only for numbers making other numbers.
Beginning & literate concepts (preschool - adult) Adapt according to level
- Mathematical ideas build upon each other.
- Mathematical ideas are connected to other mathematical ideas.
- Mathematical ideas are connected to the world.
Educator notes
Problem solving
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Smart people just know how solve problems.
- Use key words to solve word problems.
Beginning & literate concepts (preschool - adult) Adapt according to level
- Problems are solved with a heuristic, a repertoire of strategies, meta cognition or reflection, and persistence.
- A heuristic is a series of generalized steps.
- It is helpful to know and use a problem solving heuristic to solve problems, think about what you know or have done and what you need to find out or do.
- Problems can be solved with different strategies.
- Use manipulatives to represent objects and actions in the problem.
- Work a simpler problem.
- Trial and error, guess and check.
- Work backwards
- Use smaller numbers
- Use systematic steps.
- Look for, recognize and describe patterns: quantity, AB/AB, ABBA/ABBA, size, area, volume, rotation, shading, shape, position, subtraction, addition, reflection, multiplication, analogy, and recursive
- Break a problem into two related problems and solve the original problem in two steps: one for each problem.
- Act out the problem. Physically or mentally.
- Use a pictures, graphical representation - model, drawing picture or diagram
- Problems can be solved with models and equations.
- Categorize information to find relationships and patterns that will assist reasoning and proof.
- Organize data to look for patterns sequence, chart, table, making a graph, Venn diagrams, and dichotomous key.
- Process of elimination or process of identification
- Write an open sentence
- Use algebraic reasoning
- Use logical reasoning: matrices, deductive, inductive, truth tables
- Brainstorming
- Use equivalent numbers 3/5, 6/10, 60/100, .6, 60%
- It's good to monitor and reflect on the process of mathematical problem solving and regulate our actions.
- It's good to develop the habit and ability to monitor and regulate our thinking processes and actions when solving problems.
- Meta cognition (self talk) and group discussion is helpful to talk through a problem to solve it and reflect on the accuracy of the process and solution.
- The more problems I solve (persistence) the easier it is to solve problems and use mathematics.
- Some habits of mind are more conducive for solving problems than others.
- Algorithm is a step by step list of instructions to solve a type of problems or task.
Strategies for solving problems
Educator notes
Reasoning and Proof
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Ideas just pop into your mind.
- Reasoning in math is knowing to +, -, *, or /.
Beginning & literate concepts (preschool - adult) Adapt according to level
- Reasoning begins with examination, comparison, and evaluation.
- Examination can include discovering similarities and differences to organize, categorize, seriate, make connections, create correspondences and create other structures. All which can be connected for deeper understanding and to solve problems.
- Organizing similar problems with their solutions may provide examples to use to generalize patterns, explanations, expressions to describe conditions in which the mathematical ideas are valid.
- When expressions, equations, or procedures are deemed valid in enough specific situations, usually the next step is to see if the method is valid for all instances (infinite).
- A procedure or equation may be verified or proven if a reason can be given for every possible solution.
- Conjecture is an unproven statement, believed to be true, but under threat of being disproven by counterexample. It may be based on an idea or conclusion with insufficient evidence or reason to prove. As such it can be a starting point for a proof to be proven true or false.
- Axiom is alogical statement assumed to be true, or self-evident.
- One counter example will disprove a conjecture.
- When explaining a proof a reason needs to be given for every change made.
- Pictures and charts can be used to help support reasoning and proof.
- Numbers can be compared by by thinking of their values on a balance (equal arm balance) and changing the numbers on either side until it is balanced.
- Numbers can be made equal by thinking of their values on a balance (equal arm balance) and changing the numbers on either side until it is balanced.
- Changes to those numbers are created with the mathematical operations.
Educator notes
Big Ideas to unpack & map - Source Science for All Americans
- Some aspects of reasoning have clear logical rules, others have only guidelines, and still others have almost unlimited room for creativity (and, of course, error). A convincing argument requires both true statements and valid connections among them. Yet formal logic concerns the validity of the connections among statements, not whether the statements are actually true. It is logically correct to argue that if all birds can fly and penguins are birds, then penguins can fly. But the conclusion is not true unless the premises are true: Do all birds really fly, and are penguins really birds? Examination of the truth of premises is as important to good reasoning as the logic that operates on them is. In this case, because the logic is correct but the conclusion is false (penguins cannot fly), one or both of the premises must be false (not all birds can fly, and/or penguins are not birds).
- Very complex logical arguments can be built from a small number of logical steps, which hang on precise use of the basic terms "if," "and," "or," and "not." For example, medical diagnosis involves branching chains of logic such as "If the patient has disease X or disease Y and also has laboratory result B, but does not have a history of C, then he or she should get treatment D." Such logical problem solving may require expert knowledge of many relationships, access to much data to feed into the relationships, and skill in deducing branching chains of logical operations. Because computers can store and retrieve large numbers of relationships and data and can rapidly perform long series of logical steps, they are being used increasingly to help experts solve complex problems that would otherwise be very difficult or impossible to solve. Not all logical problems, however, can be solved by computers.
- Logical connections can easily be distorted. For example, the proposition that all birds can fly does not imply logically that all creatures that can fly are birds. As obvious as this simple example may seem, distortion often occurs, particularly in emotionally charged situations. For example: All guilty prisoners refuse to testify against themselves; prisoner Smith refuses to testify against himself; therefore, prisoner Smith is guilty.
- Distortions in logic often result from not distinguishing between necessary conditions and sufficient conditions. A condition that is necessary for a consequence is always required but may not be enough in itself—being a U.S. citizen is necessary to be elected president, for example, but not sufficient. A condition that is sufficient for a consequence is enough by itself, but there may be other ways to arrive at the same consequence—winning the state lottery is sufficient for becoming rich, but there are other ways. A condition, however, may be both necessary and sufficient; for example, receiving a majority of the electoral vote is both necessary for becoming president and sufficient for doing so, because it is the only way.
- Logic has limited usefulness in finding solutions to many problems. Outside of abstract models, we often cannot establish with confidence either the truth of the premises or the logical connections between them. Precise logic requires that we can make declarations such as "If X is true, then Y is true also" (a barking dog does not bite), and "X is true" (Spot barks). Typically, however, all we know is that "if X is true, then Y is often true also" (a barking dog usually does not bite) and "X seems to be approximately true a lot of the time" (Spot usually barks). Commonly, therefore, strict logic has to be replaced by probabilities or other kinds of reasoning that lead to much less certain results—for example, to the claim that on average, rain will fall before evening on 70 percent of days that have morning weather conditions similar to today's.
- If we apply logical deduction to a general rule (all feathered creatures fly), we can produce a conclusion about a particular instance or class of instances (penguins fly). But where do the general rules come from? Often they are generalizations made from observations—finding a number of similar instances and guessing that what is true of them is true of all their class ("every feathered creature I have seen can fly, so perhaps all can"). Or a general rule may spring from the imagination, by no traceable means, with the hope that some observable aspects of phenomena can be shown to follow logically from it (example: "What if it were true that the sun is the center of motion for all the planets, including the earth? Could such a system produce the apparent motions in the sky?").
- Once a general rule has been hypothesized, by whatever means, logic serves in checking its validity. If a contrary instance is found (a feathered creature that cannot fly), the hypothesis is not true. On the other hand, the only way to prove logically that a general hypothesis about a class is true is to examine all possible instances (all birds), which is difficult in practice and sometimes impossible even in principle. So it is usually much easier to prove general hypotheses to be logically false than to prove them to be true. Computers now sometimes make it possible to demonstrate the truth of questionable mathematical generalizations convincingly, even if not to prove them, by testing enormous numbers of particular cases.
- Science can use deductive logic if general principles about phenomena have been hypothesized, but such logic cannot lead to those general principles. Scientific principles are usually arrived at by generalizing from a limited number of experiences—for instance, if all observed feathered creatures hatch from eggs, then perhaps all feathered creatures do. This is a very important kind of reasoning even if the number of observations is small (for example, being burned once by fire may be enough to make someone wary of fire for life). However, our natural tendency to generalize can also lead us astray. Getting sick the day after breaking a mirror may be enough to make someone afraid of broken mirrors for life. On a more sophisticated level, finding that several patients having the same symptoms recover after using a new drug may lead a doctor to generalize that all similar patients will recover by using it, even though recovery might have occurred just by chance.
- The human tendency to generalize has some subtle aspects. Once formed, generalities tend to influence people's perception and interpretation of events. Having made the generalization that the drug will help all patients having certain symptoms, for example, the doctor may be likely to interpret a patient's condition as having improved after taking the drug, even if that is doubtful. To prevent such biases in research, scientists commonly use a "blind" procedure in which the person observing or interpreting results is not the same person who controls the conditions (for instance, the doctor who judges the patient's condition does not know what specific treatment that patient received).
- Much of reasoning, and perhaps most of creative thought, involves not only logic but analogies. When one situation seems to resemble another in some way, we may believe that it resembles it in other ways too. For example, light spreads away from a source much as water waves spread from a disturbance, so perhaps light acts like water waves in other ways, such as producing interference patterns where waves cross (it does). Or, the sun is like a fire in that it produces heat and light, so perhaps it too involves burning fuel (in fact, it does not). The important point is that reasoning by analogy can suggest conclusions, but it can never prove them to be true.
Representation
relates to
Relative position and motion (science cross-cutting)
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Objects are always relative to me.
- It doesn't matter if a person changes position, because people understand what I mean.
Beginning & literate concepts (preschool - adult) Adapt according to level
Representation (also communication)
- Representations help organize, record, and communicate mathematical ideas.
- Representations help solve problems.
- Mathematical ideas are represented externally and internally.
- Mathematical ideas are represented with object and actions with those objects.
- The representation, null and zero are special representations of the lack of objects or ideas.
- All mathematical representations are connected to physical entities.
- When representing values graphically the use of a scale and units helps to visualize that representation and to do so more accurately and proportionally. For example the difference between six feet and ten feet is four. The difference between 72 inches and 120 inches is 48. How each are represented makes a difference as to communicating the equality or not.
- Tables, charts, and graphs can be used to represent objects and events.
- Graphs can be used to identify and represent relationships.
Relative position
- An object's position can change.
- An object is located relative to a reference object.
- Objects can be located with different combinations of distances and directions from a singular point or multiple points. (one point as a reference object can be used to locate another point or object with a distance and direction.) (An object or point can be located from two know points with a distance and direction from one point and either a distance or a direction from the second point.)
Relative motion
- Objects move in different ways (straight, crocked, circular, and back and forth).
- Objects move fast and slow.
- An object's motion can be described by tracing and measuring its position over time.
- Motion is relative to a reference point.
- Motion can be too fast or slow for people to see.
- Objects move steadily or change direction.
- Objects that vibrate is motion that is relative to itself. See sound.
- Motion of an object can be described by its position, direction of motion, and speed.
- Motion can be measured and represented on a graph.
- Motion and force are often related. See force.
Educator notes
Variables
Misconceptions and concepts
Initial perceptual naive misconceptions (any age)
(Explanations for people's misconceptions: naive understandings & perceptual responses)
- Objects change because they want to or people wish they would.
Beginning concepts (preschool - 7 years)
- Variable is a property that changes.
- Results can be changed by changing what and how objects interact.
Literate concepts (middle level to adult)
- Properties can be made into variables by determining a range through which they can vary.
- Variables are conditions that change.
- Variables need to be controlled for an experiment to be a fair comparison.
- A controlled experiment is one with all the conditions (variables) the same except the one that is being tested.
- Identifying, selecting, controlling, and manipulating variables is central to experimentation.
Advanced concepts
Educator notes
Focus questions.
- If x has only one solution, is it a variable?
- Are variables nouns or what?
Math home page